题目内容
14. 如图所示,空气中有一点光源S到玻璃平行砖上表面的垂直距离为d,玻璃砖的厚度为$\frac{{\sqrt{3}}}{2}d$,从S发出的光线SA以入射角θ=45°入射到玻璃砖上表面,经过玻璃砖后从下表面射出.已知沿此光线传播的光从光源S到玻璃砖上表面的传播时间与在玻璃砖中传播时间相等.求此玻璃砖的折射率n和相应的临界角C?
如图所示,空气中有一点光源S到玻璃平行砖上表面的垂直距离为d,玻璃砖的厚度为$\frac{{\sqrt{3}}}{2}d$,从S发出的光线SA以入射角θ=45°入射到玻璃砖上表面,经过玻璃砖后从下表面射出.已知沿此光线传播的光从光源S到玻璃砖上表面的传播时间与在玻璃砖中传播时间相等.求此玻璃砖的折射率n和相应的临界角C?
分析 根据公式t=$\frac{s}{v}$,$v=\frac{c}{n}$,结合几何关系,及光的折射定律,求得折射率,再由临界角定义可得:$n=\frac{1}{sinC}$,即可求解.
解答 解:据题意得光从光源S到玻璃砖上表面的传播时间:${t}_{1}=\frac{d}{ccos45°}$
光在玻璃砖中的传播速度:$v=\frac{c}{n}$
设光进入玻璃砖的折射角为γ,光在玻璃砖中传播时间:${t_2}=\frac{{\frac{{\sqrt{3}}}{2}d}}{vcosγ}$
由折射定律得:n=$\frac{sin45°}{sinγ}$
由于t1=t2,所以联立以上各式解得:γ=30°,$n=\sqrt{2}$
又根据临界角定义可得:$n=\frac{1}{sinC}$
所以可得:C=45°
答:此玻璃砖的折射率$\sqrt{2}$和相应的临界角45°.
点评 考查光的折射定律的内容,掌握临界角与折射率的关系,及传播速度与折射率的关系,注意几何关系的正确建立,也是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
4.下列说法正确的是( )
| A. | 气体分子单位时间内与单位面积器壁碰撞的次数,与单位体积内的分子数及气体分子的平均动能都有关 | |
| B. | 布朗运动是液体分子的运动,它说明分子永不停息地做无规则热运动 | |
| C. | 当两分子间的引力和斥力平衡时,分子势能最小 | |
| D. | 如果气体分子总数不变,使气体温度升高,则气体分子的平均动能一定增大,因此压强也必然增大 | |
| E. | 晶体不一定具有各向异性 |
2.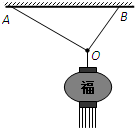 我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,轻绳能够承受足够大的拉力,则( )
我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,轻绳能够承受足够大的拉力,则( )
 我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,轻绳能够承受足够大的拉力,则( )
我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,轻绳能够承受足够大的拉力,则( )| A. | FA大于FB | |
| B. | FA、FB的合力大于mg | |
| C. | 换质量更大的灯笼,FB的增加量比FA的增加量大 | |
| D. | 无论如何调节悬点A的位置,FA、FB都不可能大于mg |
9.利用如图所示装置可以做力学中的许多实验,则下列利用此装置进行相关实验时哪一个说法是正确的?( )


| A. | 利用此装置“研究匀变速直线运动”时,必须设法消除小车和木板间摩擦阻力的影响 | |
| B. | 利用此装置探究“小车的加速度与质量的关系”并用图象法处理数据时,如果画出小车的加速度a随质量M变化的a-M图象不是直线,就可确定加速度与质量成反比 | |
| C. | 利用此装置探究“功与速度变化的关系”实验时,应将木板带打点计时器的一端适当垫高平衡摩擦力 | |
| D. | 实验时不需要调整滑轮高度,不用管细线与木板是否平行 |
19.万有引力可以理解为:任何有质量的物体都要在其周围空间产生一个引力场,一个有质量的物体在其他有质量的物体所产生的引力场中都要受到该引力场的引力(即万有引力)作用,这种情况可以与电场相类比,那么在地球产生的引力场中的重力加速度,可以与电场中下列哪个物理量相类比( )
| A. | 电场强度 | B. | 电势 | C. | 电势能 | D. | 电场力 |
6.小灯泡灯丝的电阻会随温度的升高而变大.某同学为研究这一现象,用实验得
到如下数据(I和U分别小灯泡上的电流和电压):
(1)在如图1框中画出实验电路图.可用的器材有:电压表、电流表、滑线变阻器(变化范围0-10Ω)、电源、小灯泡、电键、导线若干.

(2)在图2中画出小灯泡的U-I曲线.
(3)如图3所示,用一个定值电阻R和两个上述小灯泡组成串并联电路,连接到内阻不计、电动势为3V的电源上.已知流过电阻R的电流是流过灯泡b电流的两倍,则流过灯泡b的电流约为0.07A.
| U(V) | 0.0 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| I(A) | 0.000 | 0.050 | 0.100 | 0.150 | 0.180 | 0.195 | 0.205 | 0.215 |
(1)在如图1框中画出实验电路图.可用的器材有:电压表、电流表、滑线变阻器(变化范围0-10Ω)、电源、小灯泡、电键、导线若干.

(2)在图2中画出小灯泡的U-I曲线.
(3)如图3所示,用一个定值电阻R和两个上述小灯泡组成串并联电路,连接到内阻不计、电动势为3V的电源上.已知流过电阻R的电流是流过灯泡b电流的两倍,则流过灯泡b的电流约为0.07A.
3.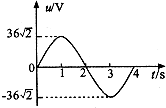 矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
 矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 交流电压的有效值为36$\sqrt{2}$V | |
| B. | 交流电压的最大值为36$\sqrt{2}$V,频率为50Hz | |
| C. | 2s末线框平面垂直于磁场,通过线框的磁通量最大 | |
| D. | 1s末线框平面垂直于磁场,通过线框的磁通量变化最快 |
17. 如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )
如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )
 如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )
如图所示,X是未知放射源,M是电场,L是薄铝片,D是计数器.现将强电场M移开,计数器所记录的计数率保侍不变,其后再将薄铝片L移开,则见计数率大幅度上升,则X为( )| A. | 纯β放射源 | B. | 纯γ放射源 | ||
| C. | α及β的混合放射源 | D. | α及γ的混合放射源 |
 如图,用细线线拴住质量分别为m1、m2的小球a、b并悬挂在天花板下,平衡时两球心在同一水平面上且距天花板的距离为L.将a拉至水平位置后由静止释放,在最低位置时与b发生弹性正碰,若碰后两球上升的最大高度相同.重力加速度为g.求:m1与m2的比值及碰后两球各自的速度大小.
如图,用细线线拴住质量分别为m1、m2的小球a、b并悬挂在天花板下,平衡时两球心在同一水平面上且距天花板的距离为L.将a拉至水平位置后由静止释放,在最低位置时与b发生弹性正碰,若碰后两球上升的最大高度相同.重力加速度为g.求:m1与m2的比值及碰后两球各自的速度大小.