题目内容
12.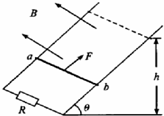 在倾角为θ的两平行光滑长直金属导轨的下端,接有一电阻R,导轨自身的电阻可忽略不计,有一磁感应强度为B的匀强磁场与两金属导轨平面垂直,方向垂直于导轨面向上.质量为m,电阻为r长度为 L 的金属棒ab,在沿着导轨面且与棒垂直的恒力F作用下沿导轨以速度 V 匀速上滑,上升高度为h,如图所示.则在此过程中( )
在倾角为θ的两平行光滑长直金属导轨的下端,接有一电阻R,导轨自身的电阻可忽略不计,有一磁感应强度为B的匀强磁场与两金属导轨平面垂直,方向垂直于导轨面向上.质量为m,电阻为r长度为 L 的金属棒ab,在沿着导轨面且与棒垂直的恒力F作用下沿导轨以速度 V 匀速上滑,上升高度为h,如图所示.则在此过程中( )| A. | 通过电阻R的电流为:$\frac{BLV}{R+r}$ | |
| B. | 恒力F在数值上等于mgsinθ+$\frac{{B}^{2}{L}^{2}V}{R+r}$ | |
| C. | 恒力F与重力的合力对金属棒ab所做的功等于零 | |
| D. | 恒力F对金属棒ab所做的功等于电阻R上释放的焦耳热 |
分析 依据切割感应电动势E=BLv,及闭合电路欧姆定律,I=$\frac{E}{R+r}$,即可求解;
导体棒匀速上升,因此合外力为零,对导体棒正确受力分析,由平衡条件求出恒力F的大小.
根据动能定理列方程,弄清功能转化关系,注意克服安培力所做功即为回路电阻中产生的热量.
解答 解:A、依据切割感应电动势E=BLv,及闭合电路欧姆定律,I=$\frac{E}{R+r}$=$\frac{BLV}{R+r}$,故A正确.
B、导体棒匀速上升过程中,在斜面方向上受到恒力F和沿斜面向下的重力的分力mgsinθ和安培力,依据平衡条件,则有F=mgsinθ+$\frac{{B}^{2}{L}^{2}V}{R+r}$,故B正确.
CD、根据动能定理得:WF-WG-W安=0,即WF-WG=W安,即恒力F与重力的合力对金属棒ab所做的功等于金属棒克服安培力做功,而金属棒克服安培力所做功即为回路电阻中产生的热量,故有:恒力F与重力的合力所做的功等于电阻R上发出的焦耳热,故CD错误.
故选:AB.
点评 对于电磁感应与功能结合问题,注意利用动能定理进行判断各个力做功之间关系,尤其注意的是克服安培力所做功等于整个回路中产生热量,同时掌握法拉第电磁感应定律与闭合电路欧姆定律的内容.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.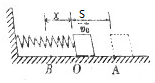 如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
 如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )| A. | $\frac{1}{2}m{v}_{0}^{2}$ | B. | $\frac{1}{2}$kx2 | C. | kx2 | D. | μmgS |
7. 在匀强磁场中直角三角形线框abc以ab边为轴以角速度ω匀速转动,某时刻到如图所示位置,已知ab边的边长为L,ac边与ab边的夹角为θ,三边的电阻均为r,磁感应强度为B.下列说法正确的是( )
在匀强磁场中直角三角形线框abc以ab边为轴以角速度ω匀速转动,某时刻到如图所示位置,已知ab边的边长为L,ac边与ab边的夹角为θ,三边的电阻均为r,磁感应强度为B.下列说法正确的是( )
 在匀强磁场中直角三角形线框abc以ab边为轴以角速度ω匀速转动,某时刻到如图所示位置,已知ab边的边长为L,ac边与ab边的夹角为θ,三边的电阻均为r,磁感应强度为B.下列说法正确的是( )
在匀强磁场中直角三角形线框abc以ab边为轴以角速度ω匀速转动,某时刻到如图所示位置,已知ab边的边长为L,ac边与ab边的夹角为θ,三边的电阻均为r,磁感应强度为B.下列说法正确的是( )| A. | 此时刻线框中的磁通量为零,线框中无电流 | |
| B. | 此时c点电势高于b点电势 | |
| C. | 此时电动势大小为$\frac{{Bω{L^2}sinθcosθ}}{2}$ | |
| D. | 此时ab两点间电势差大小为$\frac{{2Bω{L^2}sinθcosθ}}{3}$ |
17.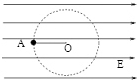 如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
 如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )| A. | $\sqrt{2gr}$ | B. | 2$\sqrt{gr}$ | C. | $\sqrt{(6-2\sqrt{2})gr}$ | D. | $\sqrt{(6+2\sqrt{2})gr}$ |
4. 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )| A. | 物体开始运动后加速度大小可以大于g | |
| B. | 物体开始运动后加速度不断减小 | |
| C. | 经过时间t=$\frac{mg}{μkq}$,物体在竖直墙壁上的位移达到最大值 | |
| D. | 经过时间t=$\frac{mg}{μkq}$,物体运动速度达最大值 |
 如图所示,一矩形线圈在匀强磁场中绕OO′轴匀速转动,磁场方向与转轴垂直.线圈匝数n=40,电阻r=0.1Ω,长l1=0.02m,宽l2=0.04m,角速度ω=100rad/s,磁场的磁感强度B=0.2T,线圈两端外接电阻R=9.9Ω的用电器和一个交流电流表.求:
如图所示,一矩形线圈在匀强磁场中绕OO′轴匀速转动,磁场方向与转轴垂直.线圈匝数n=40,电阻r=0.1Ω,长l1=0.02m,宽l2=0.04m,角速度ω=100rad/s,磁场的磁感强度B=0.2T,线圈两端外接电阻R=9.9Ω的用电器和一个交流电流表.求: 如图所示,正点电荷其中的一条电场线与x轴重合,一带正电的粒子从x轴上的a点由静止开始仅在电场力作用下运动到b点.在此运动过程中,下列关于粒子运动速度v随时间t的变化,电场强度E和运动径迹上电势φ、粒子的电势能EP随位移x的变化图象可能正确的是( )
如图所示,正点电荷其中的一条电场线与x轴重合,一带正电的粒子从x轴上的a点由静止开始仅在电场力作用下运动到b点.在此运动过程中,下列关于粒子运动速度v随时间t的变化,电场强度E和运动径迹上电势φ、粒子的电势能EP随位移x的变化图象可能正确的是( )



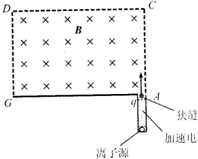 利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.
利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用. 如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速率、质量为m的电子.若极板长为L,间距为d.当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离A板垂直距离为$\frac{3}{4}$d.以已知电子的电荷量为e,L=2d,不计电子重力与它们之间的相互作用力.
如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速率、质量为m的电子.若极板长为L,间距为d.当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离A板垂直距离为$\frac{3}{4}$d.以已知电子的电荷量为e,L=2d,不计电子重力与它们之间的相互作用力.