题目内容
2．甲、乙两船的质量均为M，它们都静止在平静的湖面上，质量为M的人从甲船跳到乙船上，再从乙船跳回甲船，经过多次跳跃后，最后人停在乙船上，假设人的阻力可忽略，则（ ）| A． | 两船 （包括人）的动量之和为零 | B． | 两船（包括人）的动量相同 | ||
| C． | 甲、乙两船的速度大小之比为1：2 | D． | 因跳跃次数未知，故无法判断 |
分析 水的阻力忽略不计，在人跳跃过程中，对甲、乙两船和人组成的系统动量守恒，由动量守恒定律求出甲乙两船的速度大小和动量大小之比，根据动量守恒定律求出系统的总动量．
解答 解：A、以人与两船组成的系统为研究对象，人在跳跃过程中系统的总动量守恒，初态系统的总动量为零，所以两船 （包括人）的动量之和保持为零，故A正确．
BCD、系统的总动量为零，由动量守恒定律知：甲船与乙船（包括人）的动量大小之比是1：1，而动量的方向相反，所以甲船与乙船（包括人）的动量不同．由P=mv，知甲、乙两船的速度与质量成反比，所以甲、乙两船的速度大小之比为2：1．故BCD错误．
故选：A
点评 解决的关键是要知道人、两船系统总动量守恒，总动量为零，对系统运用动量守恒定律进行分析．
练习册系列答案
阅读快车系列答案
相关题目
16．
氢原子能级的示意图如图所示，氢原子从n=4的能级跃迁到n=2的能级时辐射出可见光a，从n=3的能级跃迁到n=2的能级时辐射出可见光b，按玻尔的理论，下列说法错误的是（ ）
氢原子能级的示意图如图所示，氢原子从n=4的能级跃迁到n=2的能级时辐射出可见光a，从n=3的能级跃迁到n=2的能级时辐射出可见光b，按玻尔的理论，下列说法错误的是（ ）| A． | a光的光子能量大于b光的光子能量 | |
| B． | 氢原子处于n=1的能级时，核外电子离原子核最近 | |
| C． | 在真空中传播时，b光的波长较短 | |
| D． | 氢原子处于n=4的能级时，核外电子动能小于处于n=2的能级时核外电子的动能 |
如图所示，匝数为50匝、面积为0.02m2的线圈，处于磁感应强度为B1=$\frac{1}{π}$T的匀强磁场中．当线圈绕O1O2以ω为10πrad/s匀速转动时，电压表、电流表的读数分别为7V、1A．电动机的内阻r为1Ω，用绝缘绳牵引一根原来静止的长L为1m、质量m为0.2kg的导体棒MN沿轨道上升．导体棒的电阻R为1Ω，架在倾角为30°的框架上，它们处于方向与框架平面垂直、磁感应强度为B2=1T的匀强磁场中．当导体棒沿轨道上滑1.6，m时获得稳定的速度，所用的时间为1s．不计框架电阻及一切摩擦，g取10m/s2．求：
如图所示，“冰雪游乐场”滑道由光滑的曲面滑道AB和粗糙的水平滑道BC构成，AB滑道与BC滑道在B点平滑连接．一小孩乘坐冰车从滑道顶端A点由静止滑下，在曲面滑道的末端B点与处于静止状态的家长所坐的冰车发生碰撞，碰撞后小孩及其冰车恰好停止运动，家长及其冰车最终停在水平滑道的C点．已知曲面滑道AB的竖直高度h=3.2m，小孩和冰车的总质量m=30kg，家长和冰车的总质量为M=60kg，人和冰车可视为质点，重力加速度g取10m/s2．求：
14．图甲为一列简谐横波在t=0.10s时刻的波形图，P是平衡位置为x=1m处的质点，Q是平衡位置为x=4m处的质点，图乙为质点Q的振动图象，则（ ）
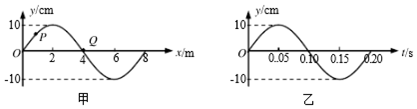
| A． | t=0.15s时，质点Q的加速度达到负向最大 | |
| B． | 从t=0.10s到t=0.25s，Q质点沿x轴负方向运动了6m | |
| C． | t=0.15s时，质点P的运动方向沿y轴负方向 | |
| D． | 从t=0.10s到t=0.25s，质点P通过的路程为30cm |
11．已知氦离子（He+）的能级图如图所示，根据能级跃迁理论可知（ ）
| A． | 氦离子（He+）从n=4能级跃迁到n=3能级比从n=3能级跃迁到n=2能级辐射出光子的频率低 | |
| B． | 大量处在n=3能级的氦离子（He+）向低能级跃迁，只能发出2种不同频率的光子 | |
| C． | 氦离子（He+）处于n=1能级时，能吸收45eV的能量跃迁到n=2能级 | |
| D． | 氦离子（He+）从n=3能级跃迁到n=2能级比从n=4能级跃迁到n=2能级辐射出的光容易衍射 |