题目内容
13.如图所示,光滑水平地面上依次放置着质量m=0.08kg的10块完全相同的长木板.一质量M=1.0kg、大小可忽略的小铜块以初速度v0=6.0m/s从长木板左侧滑上木板,当铜块滑离第一块木板时,铜块速度v1=4.0m/s.铜块最终停在第二块木板上.(取g=10m/s2,结果保留两位有效数字)求:
(1)第一块木板最终速度v2和铜块的最终速度v3;
(2)小铜块滑过第一块木板的过程中系统产生的热量.
(3)如果小铜块滑过第一块木板的时间为t=1s,则摩擦因数应该为多少?每一块板长为多少?
分析 (1)铜块和10个长木板组成的系统,在水平方向上不受力,系统动量守恒,根据动量守恒定律求出第一块木板的最终速度.铜块最终停在第二块木板上,与剩余的9个木板具有相同的速度,对铜块和剩余的9个木板为研究系统,运用动量守恒定律求出铜块的最终速度.
(2)系统损失的动能转化为内能,由此即可求出发热量.
(3)以10块长木板为研究对象,在小铜块滑过第一块木板的过程中,运用动量定理列式,可求得摩擦因数.由功能关系求每一块板长.
解答 解:(1)铜块和10个长木板在水平方向不受外力,所以系统动量守恒.
设铜块滑离第一块木板时,第一块木板的最终速度为v2,选取向右为正方向,由动量守恒定律得:
Mv0=Mv1+10mv2
代入数据解得:v2=2.5 m/s.
由题可知,铜块最终停在第二块木板上,设铜块的最终速度为v3,由动量守恒定律得:
Mv1+9mv2=(M+9m)v3
代入数据解得:v3=3.4 m/s.
(2)小铜块滑过第一块木板的过程中,系统产生的热量为:
Q=$\frac{1}{2}$Mv02-$\frac{1}{2}$Mv12-$\frac{1}{2}•$10mv22=$\frac{1}{2}$×1×6.02-$\frac{1}{2}$×1×42-5×0.08×2.52=7.5J
(3)小铜块滑过第一块木板的过程,以10块长木板为研究对象,由动量定理得:
μMgt=10mv2-0
代入数据解得:μ=0.2
由 Q=μMgL,得每一块板长为:L=3.75m
答:(1)第一块木板最终速度v2和铜块的最终速度v3分别为2.5 m/s和3.4 m/s.
(2)小铜块滑过第一块木板的过程中系统产生的热量是7.5J.
(3)摩擦因数应该为0.2,每一块板长为3.75m.
点评 本题是滑块在木板上的运动类型,解决本题的关键知道动量守恒的条件,以及能够合适地选择研究的系统,运用动量守恒定律进行求解.

| A. | 合运动的速度一定大于任一分运动的速度 | |
| B. | 合运动的位移一定大于任一分运动的位移 | |
| C. | 合运动的加速度一定大于任一分运动的加速度 | |
| D. | 合运动的时间一定等于任一分运动的时间 |
 如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )
如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )| A. | P物体从A点运动到O′的过程中,P、Q速度都在增大 | |
| B. | 在P物体从A滑到B的过程中,P的机械能增加、Q的机械能减小 | |
| C. | P运动的最大速度为$\sqrt{g(L-h)}$ | |
| D. | 当物体P到达B点时,物体Q减少的机械能为2mg(L-h) |
| A. | 声波从空气中传入水中时频率不变,波长变长 | |
| B. | 做简谐运动的质点,离开平衡位置的位移相同时,加速度也相同 | |
| C. | 双缝干涉实验中,若只减小双缝到光屏间的距离,两相邻条纹间距将变大 | |
| D. | 电磁波在真空中自由传播时,其传播方向与电场强度、磁感应强度方向均垂直 | |
| E. | 电磁波可以电磁振荡产生,若波源的电磁振荡停止,空间的电磁波随即消失 |
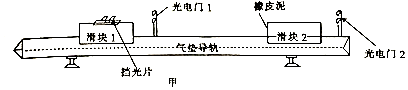
实验过程:
(1)调节气垫导轨水平,并使光电计时器系统正常工作.
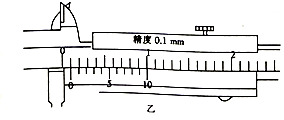
(2)在滑块1上装上挡光片,用游标卡尺测得其挡光宽度L如图乙所示,则L=1.0mm.
(3)在滑块2的碰撞端面粘上橡皮泥(或双面胶纸).
(4)用天平测出滑块1和滑块2的质量m1=0.4kg、m2=0.2kg.
(5)把滑块1和滑块2放在气垫导轨上,让滑块2处于静止状态(v2=0),用滑块1以初速度v1与之碰撞(这时光电计时器系统自动计算时间),撞后两者粘在一起,分别记下滑块1的挡光片碰前通过光电门1的挡光时间t1和碰后通过光电门2的挡光时间t2.
(6)先根据v=$\frac{L}{t}$计算滑块1碰撞前的速度v1及碰后两者的共同速度v;再计算两滑块碰撞前后的动量,并比较两滑块碰撞前后的动量的矢量和.
实验数据:(请在表格中的空白处填上相应的文字或数据)
| 次 数 | 滑块1 | 滑块2 | 碰前系统动量 (kg•m•s-1) | 碰后系统动量 kg•m•s-1 | |||
| v1/(m•s-1) | v/(m•s-1) | v2/(m•s-1) | v/(m•s-1) | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.192 | 0 | 0.192 | ① | 0 | 0.115 |
| 2 | 0.453 | 0.296 | 0 | 0.296 | ② | 0 | ③ |
| 结论:④ | |||||||
| A. | 两船 (包括人)的动量之和为零 | B. | 两船(包括人)的动量相同 | ||
| C. | 甲、乙两船的速度大小之比为1:2 | D. | 因跳跃次数未知,故无法判断 |
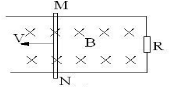 如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求:
如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求: