题目内容
13．质量为m的物体沿倾角为θ固定的斜面匀速滑下，在通过位移s的过程中（ ）| A． | 重力对物体做功mgssinθ? | |
| B． | 摩擦力对物体做正功，数值为mgssinθ? | |
| C． | 支持力对物体做功mgscosθ? | |
| D． | 合力对物体做功为0 |
分析 根据重力做功的特点求出重力所做的功；由平衡关系求得摩擦力，再由功的公式求解摩擦力的功；由动能定理可求得合力所做的功．
解答 解：A、重力对物体做功W=mgh=mgssinθ；故A正确；
B、物体匀速下滑，故摩擦力f-mgsinθ；并且摩擦力对物体做负功，大小为mgssinθ；故B错误；
C、支持力与物体的运动方向相互垂直，故支持力不做功；故C错误；
D、因物体做匀速运动，由动能定理可知，合力做功为零；故D正确；
故选：AD．
点评 本题考查动能定理及功的计算，要注意重力做功和路径无关．
练习册系列答案
相关题目
3．
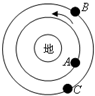三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动，mA=mB＜mC，则三颗卫星（ ）
三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动，mA=mB＜mC，则三颗卫星（ ）| A． | 线速度大小：vA＞vB=vC | |
| B． | 周期：TA＞TB=TC | |
| C． | 向心力大小：FA=FB＜FC | |
| D． | 轨道半径和周期的关系：$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
1．
如图所示，在一个顶角为2θ（θ=53°）的倒立的光滑圆锥面内，放有质量为m=1kg的小物体，小物体与竖直转轴OO’之间用与圆锥母线平行、长为L=1m的轻质细线相连．欲使细线不松弛，小物体随圆锥面一起做匀速圆周运动的角速度ω可以为（ ）（g取10m/s2，sin53°=0.8）
如图所示，在一个顶角为2θ（θ=53°）的倒立的光滑圆锥面内，放有质量为m=1kg的小物体，小物体与竖直转轴OO’之间用与圆锥母线平行、长为L=1m的轻质细线相连．欲使细线不松弛，小物体随圆锥面一起做匀速圆周运动的角速度ω可以为（ ）（g取10m/s2，sin53°=0.8）| A． | 2rad/s | B． | 3rad/s | C． | 4rad/s | D． | 5rad/s |
8．
如图所示，一小车上有一个固定的水平横杆，左边有一轻杆与竖直方向成θ角与横杆固定，下端连接一小铁球，横杆右边用一根细线吊一小铁球，当小车向右做加速运动时，细线保持与竖直方向成α角，若θ＜α，则下列说法正确的是（ ）
如图所示，一小车上有一个固定的水平横杆，左边有一轻杆与竖直方向成θ角与横杆固定，下端连接一小铁球，横杆右边用一根细线吊一小铁球，当小车向右做加速运动时，细线保持与竖直方向成α角，若θ＜α，则下列说法正确的是（ ）| A． | 轻杆对小球的弹力方向与细线平行 | |
| B． | 轻杆对小球的弹力方向沿着轻杆方向向上 | |
| C． | 轻杆对小球的弹力方向既不与细线平行，也不沿着轻杆方向 | |
| D． | 小车匀速时，θ=α |
18．关于合运动与两个分运动的关系，下列说法正确的是（ ）
| A． | 合运动的速度一定大于任一个分运动的速度 | |
| B． | 合运动的速度可能小于任一个分运动的速度 | |
| C． | 合运动的方向就是物体实际运动的方向 | |
| D． | 两个分运动的时间一定和它们合运动的时间相等 |
2．
如图所示，在水平地面上做匀速直线运动的小车，通过定滑轮用绳子吊起一个物体，若小车和被吊的物体在同一时刻的速度分别为v1和v2，绳子对物体的拉力为FT，物体所受重力为G，则下列说法正确的是（ ）
如图所示，在水平地面上做匀速直线运动的小车，通过定滑轮用绳子吊起一个物体，若小车和被吊的物体在同一时刻的速度分别为v1和v2，绳子对物体的拉力为FT，物体所受重力为G，则下列说法正确的是（ ）| A． | 物体做匀速运动，且v1=v2 | B． | 物体做加速运动，且v2＜v1 | ||
| C． | 物体做加速运动，且FT＞G | D． | 物体做匀速运动，且FT=G |
如图所示，两根金属导轨平行放置在倾角为θ=30°的斜面上，导轨下端接有定值电阻R=10Ω，导轨自身电阻忽略不计．导轨置于垂直于斜面向上的匀强磁场中，磁感应强度B=0.5T．将一根质量为m=0.1kg、电阻可不计的金属棒ab在导轨上方某处由静止释放，金属棒沿导轨下滑（金属棒ab与导轨间的摩擦不计）．设导轨足够长，导轨宽度L=2m，金属棒ab下滑过程中始终与导轨接触良好，当金属棒沿导轨下滑的高度h=3m时，速度恰好达到最大值．g=10m/s2，求：