题目内容
7. 如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求:
如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求:(1)出射电子的速率之比为vB:vC:vD;
(2)电子在磁场中运动的时间之比tB:tC:tD;
(3)E点有电子射出吗?
分析 由几何关系可知从两孔射出的粒子的运动半径,则由洛仑兹力充当向心力可得出粒子的速度关系;由周期公式及转过的角度可求得时间之比;
解答 解:磁场边长为L,粒子运动轨迹如图所示:
(1)粒子从C点离开,其半径为:rC=L,
粒子从B点离开,其半径为:rB=$\frac{L}{2}$,
粒子从D点离开,由几何关系可得:$(\frac{1}{2}{r}_{D})^{2}+{L}^{2}={r}_{D}^{2}$,
解得半径:${r}_{D}=\frac{2\sqrt{3}}{3}L$
电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=$\frac{m{v}^{2}}{r}$,
解得:r=$\frac{mv}{Be}$,
又由运动轨迹知 rC:rB:rD=6:3:4$\sqrt{3}$,
则vB:vC:vD=3:6:4$\sqrt{3}$;
(2)粒子做圆周运动的周期:T=$\frac{2πm}{Be}$,
粒子在磁场中的运动时间:t=$\frac{θ}{2π}$T.
则:tB=$\frac{1}{2}$T,tC=$\frac{1}{4}$T,tD=$\frac{1}{6}$T,则tB:tC:tD=6:3:2.
(3)粒子在磁场中,受洛伦兹力作用,运动轨迹应为圆周运动,由于AE两点在同一直线上,故粒子不可能从E点射出.
答:(1)出射电子的速率之比为3:6:4$\sqrt{3}$;
(2)电子在磁场中运动的时间之比6:3:2.
(3)不能.
点评 本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.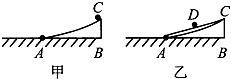 如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
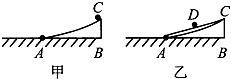 如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )| A. | v1>v2,t1>t2 | B. | v1>v2,t1=t2 | C. | v1>v2,t1<t2 | D. | v1=v2,t1=t2 |
18.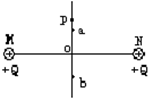 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )| A. | 点电荷-q在a、b两点的速度一定相等 | |
| B. | 点电荷-q在a、b两点的动能一定相等 | |
| C. | 点电荷-q在a、b两点的加速度一定相等 | |
| D. | 点电荷-q做简谐运动 |
2.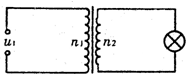 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )| A. | Um=200V | B. | Um=200$\sqrt{2}V$ | ||
| C. | 当ωt=$\frac{π}{2}$时,副线圈中的电流为O | D. | 当ωt=π时,副线圈中的电流为O |
12.某实验小组采用如图1所示的装置探究“合外力做功与速度变化的关系”.实验时平衡摩擦力后,先接通电源再松开小车,打点计时器在纸带上打下一系列点.小车所受到的拉力为0.20N,小车的质量为200g.
①某同学选取一条比较理想的纸带(图2)进行分析,小车刚开始运动时对应在纸带上的点记为起始点O,在点迹清晰段依次选取七个计数点A、B、C、D、E、F、G,相邻计数点间的时间间隔为0.1s.测量起始点O至各计数点的距离,计算计数点对应小车的瞬时速度、计数点与O点之间的速度平方差、起始点O到计数点过程中细绳对小车做的功.其中计数点D的三项数据没有计算,请完成计算并把结果填入表格中.
②以W为纵坐标、以△v2为横坐标在方格纸中作出W-△v2.图象.B、C、E、F四点已经在图中描出,请在图3中描出D点,并根据描点合理画出图象.
③根据图象分析得到的结论W与△v2成正比.
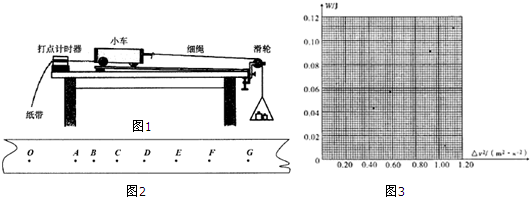
①某同学选取一条比较理想的纸带(图2)进行分析,小车刚开始运动时对应在纸带上的点记为起始点O,在点迹清晰段依次选取七个计数点A、B、C、D、E、F、G,相邻计数点间的时间间隔为0.1s.测量起始点O至各计数点的距离,计算计数点对应小车的瞬时速度、计数点与O点之间的速度平方差、起始点O到计数点过程中细绳对小车做的功.其中计数点D的三项数据没有计算,请完成计算并把结果填入表格中.
| 点迹 | O | A | B | C | D | E | F | G |
| x/cm | 15.50 | 21.60 | 28.61 | 36.70 | 45.75 | 55.75 | 66.77 | |
| v/(m•s-1) | -- | -- | 0.656 | 0.755 | -- | 0.953 | 1.051 | -- |
| △v2/(m2•S-2) | -- | 0.430 | 0.570 | 0.908 | 1.105 | -- | ||
| W/J | 0.432 | 0.0572 | 0.0915 | 0.112 |
③根据图象分析得到的结论W与△v2成正比.

12.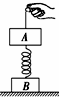 如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
 如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )| A. | 两个阶段拉力做的功相等 | |
| B. | 拉力做的总功等于A的重力势能的增加量 | |
| C. | 第一阶段,拉力做的功大于A的重力势能的增加量 | |
| D. | 第二阶段,拉力做的功等于A的重力势能的增加量 |
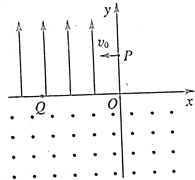 如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求:
如图所示,在xOy平面内,第二象限中有匀强电场,方向沿y轴正方向,在第四象限有匀强磁场,方向垂直于xOy平面问外.今有一个质量为m,电量为e的电子(不计重力),从y轴上的P(0,L)点以垂直于y轴、大小为v0的初速度射入电场,经电场偏转后从x轴上的Q(-2L,0)点进入磁场,并能返回到出发点P.求: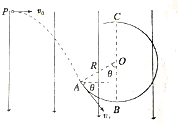 如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求:
如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求: