题目内容
9. 如图光滑斜面倾角为θ,两物体质量分别为m和M,
如图光滑斜面倾角为θ,两物体质量分别为m和M,①系统释放后m随M一起加速下滑(相对静止),求m受到的摩擦力和支持力;
②Mm间动摩擦系因数μ的取值范围;
③如果M与m间接触面光滑,求此时M与m间的作用力.
分析 (1)将物块的加速度分解为水平方向和竖直方向,根据牛顿第二定律求出物块受到的弹力和摩擦力.
(2)若保证二者相对静止,滑动摩擦力不小于水平方向的加速度和质量的成绩,根据牛顿第二定律和摩擦力公式求出动摩擦因数的取值范围.
(3)如果M与m间接触面光滑,则m竖直向下做匀加速运动,M沿斜面向下做匀加速运动,把M的加速度分解成竖直方向和水平方向的分加速度,其竖直方向的分加速度和m的加速度大小相等,根据牛顿第二定律求出弹力N.
解答 解:(1)设摩擦力为f,支持力为N,对整体分析,整体的加速度为:
$a=\frac{(M+m)gsinθ}{M+m}=gsinθ$
将加速度分解为水平方向和竖直方向,
水平方向上的加速度为:ax=acosθ=gsinθcosθ
竖直方向上的加速度为:${a}_{y}=asinθ=gsi{n}^{2}θ$
隔离对m分析,水平方向:f=max=mgsinθcosθ
竖直方向:mg-N=may,
解得:N=mgcos2θ
(2)若要保证M和m相对静止,则最大静摩擦力,即动摩擦力满足:f1≥max
f1=μmg
联立两式解得:μ≥sinθcosθ
(3)由于接触面光滑,则无摩擦力,m做竖直向下的加速运动,设m的加速度为a′,此时M与m间的作用力为N,M的加速度为a,
隔离m:mg-N=ma′
隔离M:(Mg+N)sinθ=Ma
把加速度a分解成水平方向和竖直方向上的分加速度ax、ay则
ax=acosθ
ay=asinθ
a′=ay
联立以上各式解得:N=$\frac{Mmgco{s}^{2}θ}{msi{n}^{2}θ+M}$
答:①系统释放后m随M一起加速下滑(相对静止),m受到的摩擦力为mgsinθcosθ和支持力为mgcos2θ;
②Mm间动摩擦系因数μ的取值范围为μ≥sinθcosθ;
③如果M与m间接触面光滑,此时M与m间的作用力为$\frac{Mmgco{s}^{2}θ}{msi{n}^{2}θ+M}$.
点评 本题主要考查连接体的受力分析和运动状况分析,注意灵活应用整体法和隔离法.

| A. | 仅有重力对物体做功,物体的机械能一定守恒 | |
| B. | 仅有弹力对物体做功,物体的机械能一定守恒 | |
| C. | 摩擦力对物体做的功一定等于物体机械能的变化 | |
| D. | 合外力对物体做的功一定等于物体机械能的变化 |
 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )| A. | v0≥5$\sqrt{3}$m/s | B. | v0≥0 | C. | v0>5m/s | D. | v0>5$\sqrt{2}$m/s |
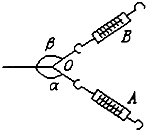 在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )
在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )| A. | 增大B的拉力,同时增大β角 | B. | 增大B的拉力,保持β角不变 | ||
| C. | 保持B的拉力大小不变,增大β角 | D. | 增大B的拉力,同时减小β角 |
| A. | 若不计声音传播的时间,井深约为20m | |
| B. | 若不计声音传播的时间,井深约为40m | |
| C. | 若考虑声音传播的时间,测量结果偏大 | |
| D. | 若考虑声音传播的时间,测量结果偏小 |
| A. |  | B. |  | C. |  | D. |  |
 如图甲所示,物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图乙所示,设最大静摩擦力与滑动摩擦力相等,重力加速度g取10m/s2,根据题目提供的信息,下列判断正确的是( )
如图甲所示,物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图乙所示,设最大静摩擦力与滑动摩擦力相等,重力加速度g取10m/s2,根据题目提供的信息,下列判断正确的是( )| A. | 物体的质量m=2kg | |
| B. | 物体与水平面间的动摩擦因数μ=0.6 | |
| C. | 物体与水平面的最大静摩擦力fmax=12N | |
| D. | 在F为10N时,物体的加速度a=2.5m/s2 |
 如图所示,竖直放置劲度系数为k的绝缘轻质弹簧,其上端与质量为m、电荷量为q 带正电的物体A相连,下端与放在水平桌面上质量也为m的绝缘物体B相连,A、B处于静止状态.现加一竖直向上的匀强电场,B恰好未离开桌面.重力加速度为g,则从加上电场到A运动到最高的过程中( )
如图所示,竖直放置劲度系数为k的绝缘轻质弹簧,其上端与质量为m、电荷量为q 带正电的物体A相连,下端与放在水平桌面上质量也为m的绝缘物体B相连,A、B处于静止状态.现加一竖直向上的匀强电场,B恰好未离开桌面.重力加速度为g,则从加上电场到A运动到最高的过程中( )| A. | A、B两物体和弹簧组成的系统机械能守恒 | |
| B. | 弹簧变为原长时A物体的动能最大 | |
| C. | 匀强电场的场强大小为$\frac{2mg}{q}$ | |
| D. | A物体电势能的减少量为$\frac{{2{m^2}{g^2}}}{k}$ |