题目内容
12.氢原子可视为电子绕着原子核(氢原子核为质子,电荷量等于一个元电荷e)做匀速圆周运动.若电子可以在距离原子核r和4r的圆轨道上做匀速圆周运动,设电子质量为m,静电力常量为k,不计质子与电子之间的万有引力,则( )| A. | 电子在距离原子核r的圆轨道上做匀速圆周运动的速度大小为$\sqrt{\frac{k}{mv}}$ | |
| B. | 电子在距离原子核r和4r的圆轨道上做匀速圆周运动的周期之比为1:8 | |
| C. | 电子在距离原子核r和4r的圆轨道上做匀速圆周运动的速度之比为2:1 | |
| D. | 电子在距离原子核r和4r的圆轨道上做匀速圆周运动的动能之比为2:1 |
分析 根据洛伦兹力提供向心力得出线速度、周期与轨道半径的表达式,从而得出速度大小之比和周期之比,结合速度之比求出动能之比.
解答 解:A、根据$k\frac{{e}^{2}}{{r}^{2}}=m\frac{{v}^{2}}{{r}^{\;}}$得,v=$\sqrt{\frac{k{e}^{2}}{mr}}$,故A错误;
B、根据$k\frac{{e}^{2}}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$得,T=$\sqrt{\frac{4{π}^{2}m{r}^{3}}{k{e}^{2}}}$,因为轨道半径之比为1:4,则周期之比为1:8,故B正确;
C、根据v=$\sqrt{\frac{k{e}^{2}}{mr}}$可知,电子在距离原子核r和4r的圆轨道上做匀速圆周运动的速度之比为2:1,故C正确;
D、根据${E}_{k}=\frac{1}{2}m{v}^{2}$可知,电子在距离原子核r和4r的圆轨道上做匀速圆周运动的动能之比为4:1,故D错误.
故选:BC
点评 根据洛伦兹力提供向心力得出线速度、周期与轨道半径的表达式,从而得出速度大小之比和周期之比,结合速度之比求出动能之比.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
3.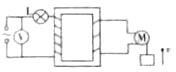 如图所示,理想变压器的原线圈接正弦交变电流,在原副线圈的回路中分别接有额定电压为U、额定功率为P的灯泡L和电动机M,电动机线圈电阻为R.原、副线圈的匝数比为2:1.当输入端接通电源后,灯泡L正常发光,且电动机正好带动一个质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
如图所示,理想变压器的原线圈接正弦交变电流,在原副线圈的回路中分别接有额定电压为U、额定功率为P的灯泡L和电动机M,电动机线圈电阻为R.原、副线圈的匝数比为2:1.当输入端接通电源后,灯泡L正常发光,且电动机正好带动一个质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
 如图所示,理想变压器的原线圈接正弦交变电流,在原副线圈的回路中分别接有额定电压为U、额定功率为P的灯泡L和电动机M,电动机线圈电阻为R.原、副线圈的匝数比为2:1.当输入端接通电源后,灯泡L正常发光,且电动机正好带动一个质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
如图所示,理想变压器的原线圈接正弦交变电流,在原副线圈的回路中分别接有额定电压为U、额定功率为P的灯泡L和电动机M,电动机线圈电阻为R.原、副线圈的匝数比为2:1.当输入端接通电源后,灯泡L正常发光,且电动机正好带动一个质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )| A. | $\frac{mgvU}{P}+\frac{4PR}{U}$ | B. | $\frac{mgvU}{P}+\frac{PR}{4U}$ | C. | $\frac{4PR}{U}$ | D. | $\frac{mgvU}{P}+\frac{4PR}{U}$+U |
17.关于做曲线运动的物体,下列说法中正确的是( )
| A. | 其加速度可以保持不变 | B. | 它所受的合外力一定是变力 | ||
| C. | 其速度可以保持不变 | D. | 其角速度大小一定变化 |
4.一小船在静水中的划速为3m/s,一条小河宽30m,水流速度为4m/s,则( )
| A. | 该小船不能渡过这条小河 | B. | 该小船不能垂直渡过这条小河 | ||
| C. | 该小船过河的最短时间为10s | D. | 该小船过河的最短时间为6s |
1. 如图所示,一半径为r的半圆形单匝线圈放在具有理想边界的匀强磁场中,磁场的磁感应强度为B.以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直),M和N是两个滑环,负载电阻为R.线圈、电流表和连接导线的电阻不计,下列说法中正确的是( )
如图所示,一半径为r的半圆形单匝线圈放在具有理想边界的匀强磁场中,磁场的磁感应强度为B.以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直),M和N是两个滑环,负载电阻为R.线圈、电流表和连接导线的电阻不计,下列说法中正确的是( )
 如图所示,一半径为r的半圆形单匝线圈放在具有理想边界的匀强磁场中,磁场的磁感应强度为B.以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直),M和N是两个滑环,负载电阻为R.线圈、电流表和连接导线的电阻不计,下列说法中正确的是( )
如图所示,一半径为r的半圆形单匝线圈放在具有理想边界的匀强磁场中,磁场的磁感应强度为B.以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直),M和N是两个滑环,负载电阻为R.线圈、电流表和连接导线的电阻不计,下列说法中正确的是( )| A. | 转动过程中电流表的示数为$\frac{{{π^2}Bn{r^2}}}{2R}$ | |
| B. | 从图示位置起转过$\frac{1}{4}$圈的时间内产生的平均感应电动势为2nπBr2 | |
| C. | 从图示位置起转过$\frac{1}{4}$圈的时间内通过负载电阻R的电荷量为$\frac{{\sqrt{2}B{π^2}{r^2}}}{8R}$ | |
| D. | 从图示位置起转过1$\frac{1}{4}$圈的时间内通过负载电阻R的电荷量为$\frac{{B{π^2}{r^2}}}{8R}$ |
 石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖.用石墨烯制作超级缆绳,人类搭建“太空电梯”的梦想有望在本世纪实现.科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换.
石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖.用石墨烯制作超级缆绳,人类搭建“太空电梯”的梦想有望在本世纪实现.科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换.
 如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°.(g取10m/s2,结果可用根式表示)
如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°.(g取10m/s2,结果可用根式表示)