题目内容
2. 研究物体从一点A由静止开始沿不同的粗糙细杆(μ已知)到圆周上各点所用的时间.
研究物体从一点A由静止开始沿不同的粗糙细杆(μ已知)到圆周上各点所用的时间.
分析 分析物体的受力情况,由牛顿第二定律确定加速度,并由几何关系来确定位移大小,从而由位移公式分析时间关系.
解答 解:设圆的直径为d,任一细杆与竖直方向的夹角为α.
对物体在细杆上的受力情况分析,由牛顿第二定律可得:mgcosα-μmgsinα=ma
得 a=gcosα-μgsinα;
根据运动学公式得 x=$\frac{1}{2}$at2
由几何关系有 x=dcosα
联立得 t=$\sqrt{\frac{2d}{g(1-μtanα)}}$
可知,细杆与竖直方向的夹角α越大,tanα越大,t越长.
答:细杆与竖直方向的夹角越大,运动到圆周上各点所用的时间越长.
点评 本题根据牛顿第二定律与运动学公式结合,得出运动的时间与细杆倾角的关系是解题的关键.

练习册系列答案
相关题目
14.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,图乙为质点Q的振动图象,则( )
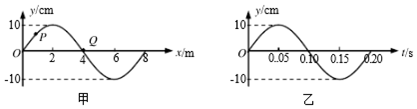

| A. | t=0.15s时,质点Q的加速度达到负向最大 | |
| B. | 从t=0.10s到t=0.25s,Q质点沿x轴负方向运动了6m | |
| C. | t=0.15s时,质点P的运动方向沿y轴负方向 | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm |
13.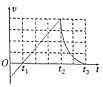 如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
 如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )
如图所示为某跳水运动员自离开跳板开始计时的速度与时间关系图象,假设空气阻力忽略不计,根据图象可知( )| A. | t2时刻运动员到达起跳的最高点 | B. | t2~t3时间内,运动员处于失重状态 | ||
| C. | 0~t2时间内,运动员机械能守恒 | D. | 0~t3时间内,合力对运动员做负功 |
17. 如图所示,物体在水平圆盘上,与圆盘一起(未发生相对滑动)绕竖直固定轴做匀速圆周运动,下列说法正确的是( )
如图所示,物体在水平圆盘上,与圆盘一起(未发生相对滑动)绕竖直固定轴做匀速圆周运动,下列说法正确的是( )
 如图所示,物体在水平圆盘上,与圆盘一起(未发生相对滑动)绕竖直固定轴做匀速圆周运动,下列说法正确的是( )
如图所示,物体在水平圆盘上,与圆盘一起(未发生相对滑动)绕竖直固定轴做匀速圆周运动,下列说法正确的是( )| A. | 物块处于受力平衡状态 | |
| B. | 圆盘角速度一定时,物块到转轴的距离越大,越容易与圆盘发生相对滑动 | |
| C. | 圆盘角速度和物块到转轴距离一定时,物块的质量越大,越容易与圆盘发生相对滑动 | |
| D. | 圆盘角速度和物块到转轴距离一定时,物块的质量越小,越容易与圆盘发生相对滑动 |
14. 如图所示,一根铝管竖直放置,把一块直径比铝管内径略小的圆柱形强磁铁从铝管上端由静止释放,可以观察到,相比磁铁自由下落,磁铁在铝管中的下落会延缓许多.关于磁铁在铝管中下落的过程,下列说法中正确的是( )
如图所示,一根铝管竖直放置,把一块直径比铝管内径略小的圆柱形强磁铁从铝管上端由静止释放,可以观察到,相比磁铁自由下落,磁铁在铝管中的下落会延缓许多.关于磁铁在铝管中下落的过程,下列说法中正确的是( )
 如图所示,一根铝管竖直放置,把一块直径比铝管内径略小的圆柱形强磁铁从铝管上端由静止释放,可以观察到,相比磁铁自由下落,磁铁在铝管中的下落会延缓许多.关于磁铁在铝管中下落的过程,下列说法中正确的是( )
如图所示,一根铝管竖直放置,把一块直径比铝管内径略小的圆柱形强磁铁从铝管上端由静止释放,可以观察到,相比磁铁自由下落,磁铁在铝管中的下落会延缓许多.关于磁铁在铝管中下落的过程,下列说法中正确的是( )| A. | 磁铁下落会延缓,主要是因为磁铁与铝管内壁有摩擦 | |
| B. | 磁铁做匀加速运动,其加速度小于重力加速度g | |
| C. | 磁铁做加速运动,其加速度逐渐增大 | |
| D. | 磁铁和铝管会产生热量,其数值等于磁铁机械能的减少量 |
11.在人类对微观世界进行探索的过程中,科学实验起到了非常重要的作用.下列说法与历史事实不符的是( )
| A. | 密立根通过油滴实验测出了基本电荷的数值 | |
| B. | 康普顿效应表明光子只具有能量,不具有动量 | |
| C. | 居里夫妇从沥青铀矿中分离出钋(Po)和镭(Ra)两种新元素 | |
| D. | 爱因斯坦在光电效应的基础上,提出了光子说 |
12. K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )
K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )
 K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )
K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成光电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法正确的是( )| A. | a光的波长一定大于b光的波长 | |
| B. | 只增加a光的强度可能使通过电流表的电流增大 | |
| C. | 只增加a光的强度可使逸出的电子最大初动能变大 | |
| D. | 阴极材料的逸出功与入射光的频率无关 |
 如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求:
如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求: