题目内容
7. 如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求:
如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑的同时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=0.75m,斜面倾角θ=37°,不计空气阻力.求:(g取10m/s2,sin37°=0.6,cos37°=0.8)
(1)小球p从A点滑到B点所需要的时间;
(2)小球q抛出时初速度的大小.
分析 (1)小球p在斜面上匀加速下滑,由牛顿第二定律求得加速度,再由运动学位移时间公式求得小球p从A点滑到B点的时间;
(2)小球q抛出做平抛运动,水平位移大小等于BC,两球运动时间相等,由q球水平方向做匀速直线运动,即可求出q抛出时初速度的大小.
解答 解:(1)小球p从斜面上下滑的加速度为a,由牛顿第二定律有:
mgsinθ=ma
设小球p从A点滑到B点所需要的时间为t1,根据运动学公式有:
l=$\frac{1}{2}a{t}_{1}^{2}$
联立解得:t1=0.5 s
(2)小球q做平抛运动,设抛出速度为v0,则:x=v0t2
由几何关系知:x=lcos37°
依题意有:t2=t1
解得:v0=1.2m/s.
答:
(1)小球p从A点滑到B点所需要的时间是0.5s;
(2)小球q抛出时初速度的大小是1.2m/s.
点评 本题是匀加速直线运动和平抛运动的综合,既要分别研究两个小球的运动情况,更要抓住它们运动的关系,如同时性、位移关系等.

练习册系列答案
相关题目
19.关于曲线运动,下列说法正确的是( )
| A. | 做曲线运动的物体所受的合力可能为零 | |
| B. | 做曲线运动的物体运动状态可能保持不变 | |
| C. | 做曲线运动的物体加速度可能不变 | |
| D. | 匀速圆周运动是一种匀变速运动 |
15. 如图所示,A是静止在赤道上随地球自转的物体,B是赤道平面内的地球同步卫星,下列关系正确的是( )
如图所示,A是静止在赤道上随地球自转的物体,B是赤道平面内的地球同步卫星,下列关系正确的是( )
 如图所示,A是静止在赤道上随地球自转的物体,B是赤道平面内的地球同步卫星,下列关系正确的是( )
如图所示,A是静止在赤道上随地球自转的物体,B是赤道平面内的地球同步卫星,下列关系正确的是( )| A. | 物体A随地球自转的线速度等于卫星B的线速度 | |
| B. | 物体A随地球自转的周期等于卫星B的周期 | |
| C. | 物体A随地球自转的角速度大于卫星B的角速度 | |
| D. | 物体A随地球自转的向心加速度等于卫星B的向心加速度 |
12.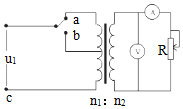 如图所示,理想变压器原副线圈的匝数比为10:1,b是原线圈的中心抽头,伏特表和安培表均为理想表,除R以外其余电阻不计.从某时刻开始在原线圈两端加上瞬时值表达式为u1=220$\sqrt{2}$sin100πt (V)的交变电压,下列说法中正确的是( )
如图所示,理想变压器原副线圈的匝数比为10:1,b是原线圈的中心抽头,伏特表和安培表均为理想表,除R以外其余电阻不计.从某时刻开始在原线圈两端加上瞬时值表达式为u1=220$\sqrt{2}$sin100πt (V)的交变电压,下列说法中正确的是( )
 如图所示,理想变压器原副线圈的匝数比为10:1,b是原线圈的中心抽头,伏特表和安培表均为理想表,除R以外其余电阻不计.从某时刻开始在原线圈两端加上瞬时值表达式为u1=220$\sqrt{2}$sin100πt (V)的交变电压,下列说法中正确的是( )
如图所示,理想变压器原副线圈的匝数比为10:1,b是原线圈的中心抽头,伏特表和安培表均为理想表,除R以外其余电阻不计.从某时刻开始在原线圈两端加上瞬时值表达式为u1=220$\sqrt{2}$sin100πt (V)的交变电压,下列说法中正确的是( )| A. | 在副线圈上瞬时值表达式为u1=22$\sqrt{2}$sin10πt(V) | |
| B. | 电压表的读数为22$\sqrt{2}$V | |
| C. | 当单刀双掷开关由a扳向b,伏特表和安培表的示数均变大 | |
| D. | 当滑动变阻器触片向上移,伏特表和安培表的示数均变小 |
19. 如图所示,质点沿x轴正方向做匀加速直线运动,t=0时经过原点O,t=0.1s时经过xa=1cm的a点,t=0.3s时经过xb=6cm的b点,由此可知,质点运动的加速度大小为( )
如图所示,质点沿x轴正方向做匀加速直线运动,t=0时经过原点O,t=0.1s时经过xa=1cm的a点,t=0.3s时经过xb=6cm的b点,由此可知,质点运动的加速度大小为( )
 如图所示,质点沿x轴正方向做匀加速直线运动,t=0时经过原点O,t=0.1s时经过xa=1cm的a点,t=0.3s时经过xb=6cm的b点,由此可知,质点运动的加速度大小为( )
如图所示,质点沿x轴正方向做匀加速直线运动,t=0时经过原点O,t=0.1s时经过xa=1cm的a点,t=0.3s时经过xb=6cm的b点,由此可知,质点运动的加速度大小为( )| A. | 1m/s2 | B. | 2m/s2 | C. | 3m/s2 | D. | 4m/s2 |
16.某种金属逸出光电子的最大初动能E km与入射光频率v的关系如图所示,下列说法正确的是( )

| A. | 当ν<ν0时,会逸出光电子 | |
| B. | 如换用其它的金属,其图线必过(v0,0)这一点 | |
| C. | 如换用其它的金属,其图线不一定与此图线平行 | |
| D. | 图中直线的斜率与普朗克常量有关 |
2.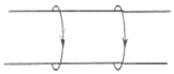 如图所示,两个相同的轻质铝环能在一个光滑的绝缘圆柱体上自由移动,设有大小不相等的电流按如图所示的方向进入两铝环,则两铝环的运动情况是( )
如图所示,两个相同的轻质铝环能在一个光滑的绝缘圆柱体上自由移动,设有大小不相等的电流按如图所示的方向进入两铝环,则两铝环的运动情况是( )
 如图所示,两个相同的轻质铝环能在一个光滑的绝缘圆柱体上自由移动,设有大小不相等的电流按如图所示的方向进入两铝环,则两铝环的运动情况是( )
如图所示,两个相同的轻质铝环能在一个光滑的绝缘圆柱体上自由移动,设有大小不相等的电流按如图所示的方向进入两铝环,则两铝环的运动情况是( )| A. | 彼此靠近,加速度变大且两者的加速度大小时刻相等 | |
| B. | 彼此靠近,两者的加速度大小和速度大小不会时刻相等 | |
| C. | 彼此远离,加速度变小且两者的加速度大小时刻相等 | |
| D. | 彼此远离,两者的加速度大小和速度大小不会时刻相等 |
 半径为R的光滑半球形碗,固定于水平桌面上,一根长为L的光滑匀质棒,一端在碗内,一端在碗外,斜靠在碗缘,求平衡时棒与水平面的夹角θ.
半径为R的光滑半球形碗,固定于水平桌面上,一根长为L的光滑匀质棒,一端在碗内,一端在碗外,斜靠在碗缘,求平衡时棒与水平面的夹角θ. 研究物体从一点A由静止开始沿不同的粗糙细杆(μ已知)到圆周上各点所用的时间.
研究物体从一点A由静止开始沿不同的粗糙细杆(μ已知)到圆周上各点所用的时间.