题目内容
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求:

(1)在A、B所形成的电场中,M点的电势ΦM.
(2)绝缘细线在C点所受到的拉力T.
答案:
解析:
解析:
|
(1)电荷E从M点运动到C的过程中,电场力做正功.根据动能定理 qU+mgL=mv2/2 得M、C两点的电势差为UMC=(mv2-2mgL)/2q 又,C点与D点为等势点,所以M点的电势为U 在C点时A对E的电场力F1与B对E的电场力F2相等,且为 F1=F2=kqQ/d2 又,A、B、C为一等边三角形,所以F1、F2的夹角为120°,故F1、F2的合力为 F12=kQq/d2,且方向竖直向下. 由牛顿运动定律得T-kQq/d2-mg=mv2/L 绝缘细线在C点所受的张力为T=kQq/d2+mg+mv2/L |

练习册系列答案
相关题目
 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v,已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v,已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: 如图所示,固定于同一条直竖直线上的A、B是两个等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B间距离为2d,MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球P,其质量为m、电荷量为+q(可视为点电荷,不影响电场分布).现将小球P从与点电荷A等高的C处由静止开始释放,小球P向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:
如图所示,固定于同一条直竖直线上的A、B是两个等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B间距离为2d,MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球P,其质量为m、电荷量为+q(可视为点电荷,不影响电场分布).现将小球P从与点电荷A等高的C处由静止开始释放,小球P向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: (2007?湖北模拟)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求:
(2007?湖北模拟)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求: (2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:
(2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: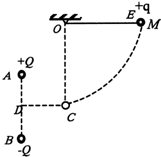 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形.另有一个带电小球E,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球 E拉起到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求:
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形.另有一个带电小球E,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球 E拉起到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求: