题目内容
5.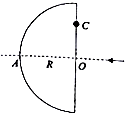 如图所示是一个半径为R的半球形透明物体的侧视图,现在有一细束单色光沿半径OA方向入射,保持入射方向不变,不考虑光线在透明物体内部的反射.
如图所示是一个半径为R的半球形透明物体的侧视图,现在有一细束单色光沿半径OA方向入射,保持入射方向不变,不考虑光线在透明物体内部的反射.①将细光束平移到距O点$\frac{\sqrt{2}}{2}$R处的c点,此时透明体左侧恰好不再有光线射出,求透明体对该单色光的折射率;
②若细光束平移到距O点0.5R处,求出射光线与OA轴线的夹角.
分析 ①透明体左侧恰好不再有光线射出时,光线发生了全反射,画出光路图,由几何关系求解临界角,从而由公式n=$\frac{1}{sinC}$求解折射率.
②光束由D点水平射入,在E点发生折射,由折射定律求出折射角,再由几何知识求解.
解答 解:①如右上图所示,光束由C处水平射入,在B处发生全反射, ∠OBC为临界角
∠OBC为临界角
由临界角公式:sinC=$\frac{\frac{\sqrt{2}}{2}R}{R}$=$\frac{\sqrt{2}}{2}$
解得:n=$\frac{1}{sinC}$=$\sqrt{2}$
②如右下图所示,光束由D点水平射入,在E点发生折射,
入射角为∠OED=α,折射角为∠NEF=β,
折射率 n=$\frac{sinβ}{sinα}$=$\sqrt{2}$
由几何关系有 sinα=$\frac{\frac{1}{2}R}{R}$=$\frac{1}{2}$
由①②解得:sinβ=$\frac{\sqrt{2}}{2}$,β=45°
由几何关系可知:∠FOE=α
∠OFE=β-α=15°或$\frac{π}{12}$
答:
①透明体对该单色光的折射率为$\sqrt{2}$;
②出射光线与OA轴线的夹角为15°.
点评 解决几何光学问题,关键要作出光路图,掌握临界条件,灵活运用数学知识,结合折射定律进行求解.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
6. A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
 A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )| A. | F1、F2大小之比为2:1 | |
| B. | F1、F2对A、B做功之比为1:2 | |
| C. | A、B质量之比为2:1 | |
| D. | 全过程中A、B克服摩擦力做功之比为2:1 |
13. 图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
 图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )| A. | 2m | B. | 0.5m | C. | 1m | D. | 1.5m |
20.如果将两个分子看成质点,当这两个分子之间的距离为r0时分子力为零,则分子力F及分子势能EP随着分子间距离r的变化而变化的情况是( )
| A. | 当r<r0时,随着r变小,F变大,EP变小 | |
| B. | 当r<r0时,随着r变小,F变大,EP变大 | |
| C. | 当r>r0时,随着r变大,F变大,EP变大 | |
| D. | 当r>r0时,随着r变大,F变小,EP变小 |
14.关于静电现象,下列说法正确的是( )
| A. | 处于静电平衡的导体,内部电势处处为零 | |
| B. | 处于静电平衡的导体,其外表面场强大小处处相等 | |
| C. | 利用尖端放电的原理,避雷针可以有效的避免建筑物遭受雷击破坏 | |
| D. | 油罐车尾部装有一条拖地的铁链,是为了把罐体上的静电及时导入大地,从而避免了火花放电 |
15. 如图所示,在“3•11”日本大地震的一次抢险救灾工作中,一架沿水平直线飞行的直升机利用降落伞匀速向下向灾区群众投放救灾物资.假设物资的总重量为G1,圆顶形降落伞伞面的重量为G2,有8条相同的拉线与物资相连,另一端均匀分布在伞的边缘上,每根拉线和竖直方向都成30°角,则每根拉线上的张力大小为( )
如图所示,在“3•11”日本大地震的一次抢险救灾工作中,一架沿水平直线飞行的直升机利用降落伞匀速向下向灾区群众投放救灾物资.假设物资的总重量为G1,圆顶形降落伞伞面的重量为G2,有8条相同的拉线与物资相连,另一端均匀分布在伞的边缘上,每根拉线和竖直方向都成30°角,则每根拉线上的张力大小为( )
 如图所示,在“3•11”日本大地震的一次抢险救灾工作中,一架沿水平直线飞行的直升机利用降落伞匀速向下向灾区群众投放救灾物资.假设物资的总重量为G1,圆顶形降落伞伞面的重量为G2,有8条相同的拉线与物资相连,另一端均匀分布在伞的边缘上,每根拉线和竖直方向都成30°角,则每根拉线上的张力大小为( )
如图所示,在“3•11”日本大地震的一次抢险救灾工作中,一架沿水平直线飞行的直升机利用降落伞匀速向下向灾区群众投放救灾物资.假设物资的总重量为G1,圆顶形降落伞伞面的重量为G2,有8条相同的拉线与物资相连,另一端均匀分布在伞的边缘上,每根拉线和竖直方向都成30°角,则每根拉线上的张力大小为( )| A. | $\frac{\sqrt{3}{G}_{1}}{12}$ | B. | $\frac{\sqrt{3}({G}_{1}+{G}_{2})}{12}$ | C. | $\frac{{G}_{1}+{G}_{2}}{8}$ | D. | $\frac{{G}_{1}}{4}$ |
 游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求:
游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求: 光电门是一种可以测量物体瞬时速度的器材
光电门是一种可以测量物体瞬时速度的器材