题目内容
1.甲、乙两颗人造地球卫星的质量之比为1:2,围绕地做匀速圆周运动的轨道半径之比为2:1.则甲、乙卫星受到的向心力大小之比为1:8,甲、乙的线速度大小之比为1:$\sqrt{2}$.分析 人造地球卫星绕地球做匀速圆周运动,由地球的万有引力提供向心力,由此列式得到向心力和线速度与轨道半径的关系式,再求解即可.
解答 解:设地球的质量为M,卫星的轨道半径为r.人造地球卫星绕地球做匀速圆周运动,由万有引力提供向心力,则有:
F=G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,
解得卫星的线速度为:v=$\sqrt{\frac{GM}{r}}$;
由F=G$\frac{Mm}{{r}^{2}}$得甲、乙卫星受到的向心力大小之比为:$\frac{{F}_{甲}}{{F}_{乙}}$=$\frac{{m}_{甲}}{{m}_{乙}}$•$\frac{{r}_{乙}^{2}}{{r}_{甲}^{2}}$=$\frac{1}{2}×$$(\frac{1}{2})^{2}$=$\frac{1}{8}$
由v=$\sqrt{\frac{GM}{r}}$得甲、乙的线速度大小之比为:$\frac{{v}_{甲}}{{v}_{乙}}$=$\sqrt{\frac{{r}_{乙}}{{r}_{甲}}}$=$\sqrt{\frac{1}{2}}$=$\frac{1}{\sqrt{2}}$
故答案为:1:8,1:$\sqrt{2}$.
点评 对于卫星问题,要建立物理模型,能抓住万有引力等于向心力这一基本思路,能灵活选择向心力的公式进行研究.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 具有各向异性的固定一定是晶体 | |
| B. | 悬浮在液体中的小颗粒越大,布朗运动越剧烈 | |
| C. | 露珠呈球状是由于液体表面张力的作用 | |
| D. | 两个分子间的引力或斥力均随分子间距的增大而减小,但斥力比引力减小得更快 | |
| E. | 把两块纯净的铅压紧,它们会“粘”在一起,说明分子间只存在分子引力 |
16.下列物理量属于矢量的是( )
| A. | 电场强度E | B. | 电流强度I | C. | 功率P | D. | 周期T |
6. 如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
 如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )| A. | A点的万有引力较大,B点的速率较大 | |
| B. | A点的万有引力较大,B点的速率较小 | |
| C. | A点的万有引力较小,B点的速率较大 | |
| D. | A点的万有引力较小,B点的速率较小 |
10.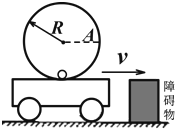 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )| A. | 铅球能上升的最大高度一定等于$\frac{{v}^{2}}{2g}$ | |
| B. | 无论v多大,铅球上升的最大高度不超过$\frac{{v}^{2}}{2g}$ | |
| C. | 要使铅球一直不脱离圆桶,v的最小速度为$\sqrt{5gR}$ | |
| D. | 若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零 |
 如图,足够长的平行玻璃砖厚度d=6cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB,一束光线以i=60°的入射角由挡板的A端射入玻璃砖,经底面反射后,恰能从挡板的B端射出,不考虑光在玻璃砖上表面的反射.已知光线在玻璃砖中的折射率n=$\sqrt{3}$,真空中的光速c=3×108m/s,求:
如图,足够长的平行玻璃砖厚度d=6cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB,一束光线以i=60°的入射角由挡板的A端射入玻璃砖,经底面反射后,恰能从挡板的B端射出,不考虑光在玻璃砖上表面的反射.已知光线在玻璃砖中的折射率n=$\sqrt{3}$,真空中的光速c=3×108m/s,求:
 如图是小飞同学在做“描绘小灯泡的伏安特性曲线”实验的实物连接图,根据题图在答题纸的方框中补全实验电路图.
如图是小飞同学在做“描绘小灯泡的伏安特性曲线”实验的实物连接图,根据题图在答题纸的方框中补全实验电路图.