题目内容
14. 质量为m=1.0kg的小滑块(可视为质点)放在质量为M=2.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.4,木板长L=3.0m.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=16N,如图所示,经一段时间后撤去F.为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间.(g取10m/s2)
质量为m=1.0kg的小滑块(可视为质点)放在质量为M=2.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.4,木板长L=3.0m.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=16N,如图所示,经一段时间后撤去F.为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间.(g取10m/s2)
分析 由题,木板上表面光滑,当木板运动时,滑块相对于地面静止不动.分析木板的运动情况,在撤去F前,木板做匀加速运动,撤去F后木板做匀减速运动.根据牛顿第二定律分别求出撤去F前后木板的加速度.由位移公式分别求出木板加速和减速运动的位移与时间的关系式.当加速和减速的总位移小于等于木板的长度时,滑块不会从木板上滑下来,求出最长的时间.
解答 解:撤去F前后木板先加速后减速.设加速过程的位移为x1,加速度为a1,加速运动的时间为t1;减速过程的位移为x2,加速度为a2,减速运动的时间为t2.由牛顿第二定律得
撤力前:F-μ(m+M)g=Ma1
代入数据解得:a1=2 m/s2
撤力后:μ(m+M)g=Ma2
代入数据解得:a2=6 m/s2
又x1=$\frac{1}{2}$a1t12,x2=$\frac{1}{2}$a2t22
为使小滑块不从木板上掉下,应满足x1+x2≤L
又a1t1=a2t2
由以上各式可解得:t1=$\frac{\sqrt{3}}{2}$ s
即作用的最长时间为$\frac{\sqrt{3}}{2}$s.
答:用水平恒力F作用的最长时间是$\frac{\sqrt{3}}{2}$s.
点评 本题首先要分析滑块与木板的运动情况,其次把握滑块不从木板上滑下的条件,即两物体之间的几何关系.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2. 固定光滑斜劈ABC置于水平面上,AC边竖直,∠A=30°,D为AC上一点,AD=BD=0.4m,如图所示,小球由A点沿AB无初速度下滑,滑到B点所用时间为(g=10m/s2)( )
固定光滑斜劈ABC置于水平面上,AC边竖直,∠A=30°,D为AC上一点,AD=BD=0.4m,如图所示,小球由A点沿AB无初速度下滑,滑到B点所用时间为(g=10m/s2)( )
 固定光滑斜劈ABC置于水平面上,AC边竖直,∠A=30°,D为AC上一点,AD=BD=0.4m,如图所示,小球由A点沿AB无初速度下滑,滑到B点所用时间为(g=10m/s2)( )
固定光滑斜劈ABC置于水平面上,AC边竖直,∠A=30°,D为AC上一点,AD=BD=0.4m,如图所示,小球由A点沿AB无初速度下滑,滑到B点所用时间为(g=10m/s2)( )| A. | $\frac{\sqrt{2}}{5}$s | B. | 0.4 s | C. | $\frac{2\sqrt{2}}{5}$s | D. | $\frac{\sqrt{3}}{5}$s |
9. 如图所示,一电场的电场线分布关于y轴(沿竖直方向)对称,O、M、N是y轴上的三个点,且OM=MN.P点在y轴右侧,MP⊥ON.下列说法正确的是( )
如图所示,一电场的电场线分布关于y轴(沿竖直方向)对称,O、M、N是y轴上的三个点,且OM=MN.P点在y轴右侧,MP⊥ON.下列说法正确的是( )
 如图所示,一电场的电场线分布关于y轴(沿竖直方向)对称,O、M、N是y轴上的三个点,且OM=MN.P点在y轴右侧,MP⊥ON.下列说法正确的是( )
如图所示,一电场的电场线分布关于y轴(沿竖直方向)对称,O、M、N是y轴上的三个点,且OM=MN.P点在y轴右侧,MP⊥ON.下列说法正确的是( )| A. | M点的电势比N点的电势高 | |
| B. | 将负电荷由O点移动到P点,电场力做正功 | |
| C. | M、N两点间的电势差小于O、M两点间的电势差 | |
| D. | 在O点静止释放一带正电粒子,该粒子将沿y轴正方向做匀加速直线运动 |
19. 一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,a,b,c三点处的电势分别为Ua,Ub,Uc,金属球上感应电荷产生的电场在球内直径上a,b,c三点的场强大小分别为Ea,Eb,Ec,则( )
一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,a,b,c三点处的电势分别为Ua,Ub,Uc,金属球上感应电荷产生的电场在球内直径上a,b,c三点的场强大小分别为Ea,Eb,Ec,则( )
 一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,a,b,c三点处的电势分别为Ua,Ub,Uc,金属球上感应电荷产生的电场在球内直径上a,b,c三点的场强大小分别为Ea,Eb,Ec,则( )
一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,a,b,c三点处的电势分别为Ua,Ub,Uc,金属球上感应电荷产生的电场在球内直径上a,b,c三点的场强大小分别为Ea,Eb,Ec,则( )| A. | Ea最大,Ua>Ub>Uc | B. | Ec最大,Ua=Ub=Uc | ||
| C. | Eb最大,Ua<Ub<Uc | D. | Ea=Eb=Ec,Ua=Ub=Uc |
6.放在粗糙水平面上的小物体,在水平拉力F作用下做加速直线运动,现将拉力F不断变小直至变为零,上述过程中该物体一直在滑动,则该物体在此过程中( )
| A. | 物体受的合外力一直在变小 | |
| B. | 加速度不断变小,速度不断变小 | |
| C. | 加速度先变大后变小,速度先变小后变大 | |
| D. | 加速度先变小后变大,速度先变大后变小 |
3.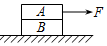 如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时,作用在A上的水平拉力F=10N,此后F逐渐增加,则在F增大到45N的过程中( )
如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时,作用在A上的水平拉力F=10N,此后F逐渐增加,则在F增大到45N的过程中( )
 如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时,作用在A上的水平拉力F=10N,此后F逐渐增加,则在F增大到45N的过程中( )
如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时,作用在A上的水平拉力F=10N,此后F逐渐增加,则在F增大到45N的过程中( )| A. | 两物体先没有相对运动,当F超过12N时,两物体开始发生相对运动 | |
| B. | 当F=16N时,B受到A的摩擦力大小等于4N | |
| C. | 两物体间始终没有发生相对运动 | |
| D. | 若拉力F作用在B上,则当F超过12N时,两物体开始发生相对运动 |
4. 如图所示,小球沿斜面向上运动,依次经过 a、b、c、d 到达最高点 e,已知 ab=bd=6m,bc=1m,小球从 a 到 c 和从 c 到 d 所用的时间都是 2s.设小球经 b、c 时的速度分别为vb、vc,则 以下错误的是( )
如图所示,小球沿斜面向上运动,依次经过 a、b、c、d 到达最高点 e,已知 ab=bd=6m,bc=1m,小球从 a 到 c 和从 c 到 d 所用的时间都是 2s.设小球经 b、c 时的速度分别为vb、vc,则 以下错误的是( )
 如图所示,小球沿斜面向上运动,依次经过 a、b、c、d 到达最高点 e,已知 ab=bd=6m,bc=1m,小球从 a 到 c 和从 c 到 d 所用的时间都是 2s.设小球经 b、c 时的速度分别为vb、vc,则 以下错误的是( )
如图所示,小球沿斜面向上运动,依次经过 a、b、c、d 到达最高点 e,已知 ab=bd=6m,bc=1m,小球从 a 到 c 和从 c 到 d 所用的时间都是 2s.设小球经 b、c 时的速度分别为vb、vc,则 以下错误的是( )| A. | vb=$\sqrt{10}$m/s | B. | vc=3m/S | ||
| C. | de=5m | D. | 从 d 到 e 所用时间为4s |
 如图所示是一列沿x轴负方向传播的波在某一时刻的波形图,此时,A点的速度方向是向下,B点速度方向是向上,在A、B、C、D四点中速度最大的点A.
如图所示是一列沿x轴负方向传播的波在某一时刻的波形图,此时,A点的速度方向是向下,B点速度方向是向上,在A、B、C、D四点中速度最大的点A. 如图,质量为m和M的物体用轻绳通过一轻质滑轮相连接,绳子足够长,不计任何摩擦.若M保持不变,m可以改变,则以下对于轻绳拉力F随m的变化图象可能正确的是( )
如图,质量为m和M的物体用轻绳通过一轻质滑轮相连接,绳子足够长,不计任何摩擦.若M保持不变,m可以改变,则以下对于轻绳拉力F随m的变化图象可能正确的是( )


