��Ŀ����
18�� ��ͼ��ʾ������A��װ��L=1.0m����ֱ���ˣ������˵�������ΪM=1.0kg�������߶Ȳ��ƣ�������������Ϊm=0.1kg��С��B��С�����֮���д�С�㶨��Ħ��������С���ӵ�����v0=4.0m/s�ij��ٶ����Ϸ��𣬸պ��ܴﵽ�˵�һ��߶ȴ���Ȼ��ʼ�ظ��½���ȡg=10m/s2��
��ͼ��ʾ������A��װ��L=1.0m����ֱ���ˣ������˵�������ΪM=1.0kg�������߶Ȳ��ƣ�������������Ϊm=0.1kg��С��B��С�����֮���д�С�㶨��Ħ��������С���ӵ�����v0=4.0m/s�ij��ٶ����Ϸ��𣬸պ��ܴﵽ�˵�һ��߶ȴ���Ȼ��ʼ�ظ��½���ȡg=10m/s2����1������С����������У�������ˮƽ���ѹ����С��
��2����С���½�������Ҫ��ʱ�䣻
��3����С����ijһ���ٶ����Ϸ���ʱ���պ��ܴﵽ�˶���û������ֱ���ˣ���С������ʱ�ij��ٶȴ�С��
���� ��1�������ٶ�λ�ƹ�ʽ���С�����ϻ����ļ��ٶȴ�С�����ţ�ٵڶ���������˺ͻ�֮���Ħ�������ٶԵ������������ݹ�����ƽ�����֧�����Ĵ�С���Ӷ��ó�������ˮƽ���ѹ����С��
��2������ţ�ٵڶ��������С���»��ļ��ٶȴ�С�����λ��ʱ�乫ʽ����½���ʱ�䣮
��3�������ٶ�λ�ƹ�ʽ���С������ʱ�ij��ٶȣ�
��� �⣺��1��С������Ĺ����У���С�������������˶��ļ��ٶȴ�СΪ��
${a}_{1}=\frac{{{v}_{0}}^{2}}{2��\frac{L}{2}}=\frac{16}{1}m/{s}^{2}=16m/{s}^{2}$��
����ţ�ٵڶ����ɵã�mg+f=ma1��
��ã�f=ma1-mg=0.1����16-10��N=0.6N��
�Ե�������������ƽ���У�N+f=Mg��
��ã�N=Mg-f=10-0.6N=9.4N��
��2��С���½������еļ��ٶȴ�СΪ��
${a}_{2}=\frac{mg-f}{m}=\frac{1-0.6}{0.1}m/{s}^{2}=4m/{s}^{2}$��
����$\frac{L}{2}=\frac{1}{2}{a}_{2}{t}^{2}$�ã�t=$\sqrt{\frac{L}{{a}_{2}}}=\sqrt{\frac{1}{4}}s=0.5s$��
��3������${v}_{0}{��}^{2}=2{a}_{1}L$�ã�${v}_{0}��=\sqrt{2{a}_{1}L}=\sqrt{2��16��1}m/s=4\sqrt{2}m/s$��
�𣺣�1��������ˮƽ���ѹ����СΪ9.4N��
��2��С���½�������Ҫ��ʱ��Ϊ0.5s��
��3��С������ʱ�ij��ٶȴ�СΪ$4\sqrt{2}$m/s��
���� ���⿼����ţ�ٵڶ����ɺ��˶�ѧ��ʽ���ۺ����ã��ؼ�����ѡ���о������ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣬��������С�����������Ħ�����ǹؼ���

| A�� | mgh+$\frac{1}{2}$mv${\;}_{0}^{2}$ | B�� | mg��H+h�� | C�� | mg��H+h��+$\frac{1}{2}$mv${\;}_{0}^{2}$ | D�� | mgH+$\frac{1}{2}$mv${\;}_{0}^{2}$ |
 ��ͼ��ʾ������������ȣ��ֱ�������硢����Ͳ�����������Ӽ��������������ͬ��ˮƽ���ٶ�v�Ⱥ�ֱ��ǿ���룬�ֱ��䵽����A��B��C������ͼ��ʾ��������˵����ȷ���У�������
��ͼ��ʾ������������ȣ��ֱ�������硢����Ͳ�����������Ӽ��������������ͬ��ˮƽ���ٶ�v�Ⱥ�ֱ��ǿ���룬�ֱ��䵽����A��B��C������ͼ��ʾ��������˵����ȷ���У�������| A�� | ����A�����磬B�����磬C������ | |
| B�� | ���������ڵ糡���˶�ʱ����� | |
| C�� | ���������ڵ糡���˶��ļ��ٶ�aA��aB��aC | |
| D�� | �������ӵ��K��ʱ�Ķ���EKA��EKB��EKC |
| A�� | ����������������α����й� | |
| B�� | �������������������� | |
| C�� | �����˶����ٶ�Խ��������Խ�� | |
| D�� | ����������������ٶ��� |
 ͼʾ�н���������A1��A2��A3�ֱ������������ȦL�͵���R���������ͬһ������Դ�ϣ������ѹ˲ʱֵΪu1=Umsin��1t���������������в�ͬ�Ķ������ֻ���һ����Դ���磬�����ѹ˲ʱֵΪu2=Umsin��2t�����Ц�2=2��1���Ļ���Դ�������������Ķ����仯����ǣ�������
ͼʾ�н���������A1��A2��A3�ֱ������������ȦL�͵���R���������ͬһ������Դ�ϣ������ѹ˲ʱֵΪu1=Umsin��1t���������������в�ͬ�Ķ������ֻ���һ����Դ���磬�����ѹ˲ʱֵΪu2=Umsin��2t�����Ц�2=2��1���Ļ���Դ�������������Ķ����仯����ǣ�������| A�� | A2��A3�Ķ������� | B�� | A1��A3�Ķ������� | C�� | A1��A3�Ķ������� | D�� | ��A1�Ķ������� |
| A�� | ����ֹ | |
| B�� | �������˶���������С��Ϊ2kg•m/s | |
| C�� | ������ͬһ�����˶� | |
| D�� | �������˶���������С��Ϊ1kg•m/s |
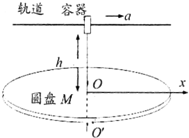 ��ͼ��ʾ��M��ˮƽ���õİ뾶�㹻���Բ�̣��ƹ���Բ�ĵ���ֱ��OO������ת�����涨����Բ��O����ˮƽ����Ϊx����������O�����Ϸ��������Ϊh=5m����һ���ɼ�ϵ�ˮ����������t=0ʱ�̿�ʼ��������ˮƽ�����x�������������ٶ�Ϊ����ȼ���ֱ���˶�����֪t=0ʱ�̵��µ�һ��ˮ���Ժ�ÿ��ǰһ��ˮ�պ��䵽����ʱ�ٵ���һ��ˮ����ȡg=10m/s2��
��ͼ��ʾ��M��ˮƽ���õİ뾶�㹻���Բ�̣��ƹ���Բ�ĵ���ֱ��OO������ת�����涨����Բ��O����ˮƽ����Ϊx����������O�����Ϸ��������Ϊh=5m����һ���ɼ�ϵ�ˮ����������t=0ʱ�̿�ʼ��������ˮƽ�����x�������������ٶ�Ϊ����ȼ���ֱ���˶�����֪t=0ʱ�̵��µ�һ��ˮ���Ժ�ÿ��ǰһ��ˮ�պ��䵽����ʱ�ٵ���һ��ˮ����ȡg=10m/s2�� ��ͼ��ʾ���ڳ�L=1m��С��A������ΪmA����ƽ��λ��O��������������ֱ�����=5��ǣ��ɾ�ֹ�ͷţ�A���°�ʱ�뾲ֹ����ƽ��λ��O�㴦��B������ΪmB��������������ײ������������ȣ��ҵ�����ǰA���ٶȵ�$\frac{1}{3}$����ײ��A���أ�B�������ڹ⻬ˮƽ������˶������ֻ������Ϊ30����㹻���Ĺ⻬б�������ȡg=10m/s2����=$\sqrt{g}$��cos5��=0.9875��B��ˮƽ���б��Ľ��㴦ʱ��е�ܵ���ʧ�����ƿ�����������
��ͼ��ʾ���ڳ�L=1m��С��A������ΪmA����ƽ��λ��O��������������ֱ�����=5��ǣ��ɾ�ֹ�ͷţ�A���°�ʱ�뾲ֹ����ƽ��λ��O�㴦��B������ΪmB��������������ײ������������ȣ��ҵ�����ǰA���ٶȵ�$\frac{1}{3}$����ײ��A���أ�B�������ڹ⻬ˮƽ������˶������ֻ������Ϊ30����㹻���Ĺ⻬б�������ȡg=10m/s2����=$\sqrt{g}$��cos5��=0.9875��B��ˮƽ���б��Ľ��㴦ʱ��е�ܵ���ʧ�����ƿ����������� ��ͼΪ����ײ�еĶ����غ㡱ʵ��װ��ʾ��ͼ
��ͼΪ����ײ�еĶ����غ㡱ʵ��װ��ʾ��ͼ