题目内容
9.如图所示,玻璃管粗细均匀,图中所示液体都是水银,已知h1=10cm,h2=5cm,大气压强P0=1.013×105Pa,纸面表示竖直平面,求下列各图中被封闭气体的压强.
分析 选择水银柱为研究对象,受力分析,根据平衡列式求解.在连通器中,同一种液体(中间不间断)同一深度处压强相等.
解答 解:(1)水银柱水平方向上受力平衡,则:P0S=P1S,即:${P}_{1}={P}_{0}=1.013×1{0}^{5}Pa$
(2)连续的水银柱的同一高度,压强相等,则:P2=${P}_{0}-ρg{h}_{1}=1.013×1{0}^{5}-13.6×1{0}^{3}×10×0.1Pa=8.77×1{0}^{4}Pa$
(3)连续的水银柱的同一高度,压强相等,则:P3=${P}_{0}-ρg{h}_{1}=1.013×1{0}^{5}-13.6×1{0}^{3}×10×0.1Pa=8.77×1{0}^{4}Pa$
(4)连续的水银柱的同一高度,压强相等,则:${P}_{4}={P}_{0}+ρ{h}_{1}g=1.013×1{0}^{5}+13.6×1{0}^{3}×0.1×10Pa=1.149×1{0}^{5}Pa$
答:下列各图中被封闭气体的压强依次为:1.013×105Pa、8.77×104Pa、8.77×104Pa、1.149×105Pa.
点评 平衡状态下气体压强的求法
(1)液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程,消去面积,得到液片两侧压强相等方程,求得气体的压强.
(2)力平衡法:选取与气体接触的液柱(或活塞)为研究对象进行受力分析,得到液柱(或活塞)的受力平衡方程,求得气体的压强.
(3)等压面法:在连通器中,同一种液体(中间不间断)同一深度处压强相等.本题采用的是等压面法.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17. 如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
 如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )
如图所示,在一根铁捧上绕有绝缘线圈,a、c是线圈两端,b为中间抽头,把a、b两点接入一平行金属导轨,b、c两点间接一电容器,在导轨上垂直导轨放一金属棒MN,导轨间有如图所示的匀强磁场,要使c点的电势高于b点的电势,则金属棒MN沿导轨的运动情况可能是( )| A. | 向右做匀加速直线运动 | B. | 向左做匀加速直线运动 | ||
| C. | 向右做匀速直线运动 | D. | 向左做匀减速直线运动 |
4.下列关于物理学中的思想和方法叙述不正确的是( )
| A. | 一个物体受到几个力共同作用产生的效果与某一个力产生的效果相同,这个力叫做那几个力的合力,这里包含了“等效替代”的思想 | |
| B. | 在“探究弹性势能的表达式”时,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为许多小段,把每一小段的弹力认为是恒力,用每小段做功的代数和代表弹力在整个过程中所做的功,这种方法叫“微元法” | |
| C. | 在探究加速度与力、质量的关系时,先保持质量不变探究加速度与力的关系,再保持力不变探究加速度与质量的关系,这种方法叫“控制变量法” | |
| D. | 根据速度定义式v=$\frac{△x}{△t}$,当△t极短时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,这种方法叫“微元法” |
14.一辆汽车运动的v-t图象如图,则汽车在0~2s内和2s~3s内相比( )
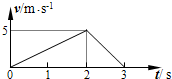

| A. | 位移大小相等 | B. | 平均速度相等 | C. | 速度变化相同 | D. | 运动方向相同 |
18.下列说法正确的是( )
| A. | 英国科学家伽利略在研究物体变速运动规律时,做了著名的“斜面实验” | |
| B. | 法拉第对电磁感应现象的研究作出了突出的贡献,他首先总结出了判断感应电流方向的规律 | |
| C. | 牛顿对物理学作出了划时代的贡献,是动力学的奠基人,所以在力学单位制中,力的单位牛顿是基本单位 | |
| D. | 元电荷e的数值最早是由物理学家密立根测得的 |
19.传感器担负着信息的采集任务,在自动控制中发挥着重要的作用.传感器能够将感受到的物理量(如温度、光、声等)转换成便于测量的量(通常是电学量),例如热敏传感器主要是应用了半导体材料制成的热敏电阻.热敏电阻阻值随温度变化的图线如图甲所示,图乙是由热敏电阻Rt作为传感器制作的简单自动报警器的电路图.下列说法正确的是( )


| A. | 为了使温度过高时报警器响铃,c应接在a处 | |
| B. | 为了使温度过高时报警器响铃,c应接在b处 | |
| C. | 若使启动报警的温度提高些,则应将滑动变阻器滑片P向左移动 | |
| D. | 如果在调试报警器达最低报警温度时,无论如何调节滑片P都不能报警,且电路无故障,可能原因是左边电源电压太低 |
 如图所示,一定质量的理想气体被活塞封闭在竖直放置的圆柱形气缸内,汽缸壁导热良好,横截面积为S的活塞可沿汽缸壁无摩擦地滑动.开始时气体压强为p,活塞下表面相对于汽缸底部的高度为h,外界的温度为T0.现缓慢地向质量可不计的活塞的上表面倒沙子,当活塞下降$\frac{h}{4}$时,外界的温度也逐渐变为T,此时气体重新达到平衡,求达到平衡时所倒沙子的质量.(已知外界大气的压强始终保持不变,重力加速度大小为g)
如图所示,一定质量的理想气体被活塞封闭在竖直放置的圆柱形气缸内,汽缸壁导热良好,横截面积为S的活塞可沿汽缸壁无摩擦地滑动.开始时气体压强为p,活塞下表面相对于汽缸底部的高度为h,外界的温度为T0.现缓慢地向质量可不计的活塞的上表面倒沙子,当活塞下降$\frac{h}{4}$时,外界的温度也逐渐变为T,此时气体重新达到平衡,求达到平衡时所倒沙子的质量.(已知外界大气的压强始终保持不变,重力加速度大小为g) 如图所示,一根有一定电阻的直导体棒质量为m、长为L,其两端放在位于水平面内间距也为L的光滑平行导轨上,并与之接触良好;棒左侧两导轨之间连接一可控电阻;导轨置于匀强磁场中,磁场的磁感应强度大小为B,方向垂直于导轨所在平面.t=0时刻,给导体棒一个平行于导轨的初速度,此时可控电阻的阻值为R0.在棒运动过程中,通过可控电阻的变化使棒中的电流强度保持恒定.不计导轨电阻,导体棒一直在磁场中
如图所示,一根有一定电阻的直导体棒质量为m、长为L,其两端放在位于水平面内间距也为L的光滑平行导轨上,并与之接触良好;棒左侧两导轨之间连接一可控电阻;导轨置于匀强磁场中,磁场的磁感应强度大小为B,方向垂直于导轨所在平面.t=0时刻,给导体棒一个平行于导轨的初速度,此时可控电阻的阻值为R0.在棒运动过程中,通过可控电阻的变化使棒中的电流强度保持恒定.不计导轨电阻,导体棒一直在磁场中 如图,质量为m的滑块从倾角为30°的固定斜面上无初速地释放后匀加速下滑,加速度a=$\frac{g}{4}$,取出发位置水平面为参考平面,能正确描述滑块的速率v、动能Ek、势能Ep、机械能E、时间t、位移s关系的是( )
如图,质量为m的滑块从倾角为30°的固定斜面上无初速地释放后匀加速下滑,加速度a=$\frac{g}{4}$,取出发位置水平面为参考平面,能正确描述滑块的速率v、动能Ek、势能Ep、机械能E、时间t、位移s关系的是( )


