题目内容
3. 如图所示,在竖直平面内有轨道ABC,其中AB段为水平直轨道,与质量m=0.5kg的小物块(可视为质点)之间的动摩擦因数μ=0.2,BC段为光滑半圆形轨道,轨道半径R=2m,轨道AB与BC在B点相切.小物块在水平拉力F=3N的作用下从A点由静止开始做匀加速直线运动,到达圆弧轨道的最低点B时撤去拉力,此时速度vB=10m/s.取g=10m/s2,则:
如图所示,在竖直平面内有轨道ABC,其中AB段为水平直轨道,与质量m=0.5kg的小物块(可视为质点)之间的动摩擦因数μ=0.2,BC段为光滑半圆形轨道,轨道半径R=2m,轨道AB与BC在B点相切.小物块在水平拉力F=3N的作用下从A点由静止开始做匀加速直线运动,到达圆弧轨道的最低点B时撤去拉力,此时速度vB=10m/s.取g=10m/s2,则:(1)拉力F做了多少功;
(2)经过B点后瞬间,物块对轨道的压力是多大;
(3)若物块从最高点C飞出后落到水平轨道上的D点(图中未画出),求BD间的距离.
分析 (1)研究物块在水平面上运动的过程,根据牛顿第二定律求出加速度,由速度位移关系公式求出AB间的距离,再由功的计算公式求解.
(2)在B点,由牛顿第二定律求出轨道对物块的支持力,再由牛顿第三定律求物块对轨道的压力.
(3)物块从B到C,运用机械能守恒定律求出物块通过C点的速度,再由平抛运动的规律求BD间的距离.
解答 解:(1)物块在水平面上运动时,由牛顿第二定律得:
F-μmg=ma
解得 a=4m/s2;
则AB间的距离 SAB=$\frac{{v}_{B}^{2}}{2a}$=12.5m
拉力F做功 W=FSAB=37.5J
(2)由牛顿第二定律 N-mg=m$\frac{{v}_{B}^{2}}{R}$
解得 N=30N
由牛顿第三定律得物块对轨道的压力 N′=N=30N
(3)从B到C的过程,由机械能守恒定律得
2mgR+$\frac{1}{2}m{v}_{C}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$
物块离开C点后做平抛运动,则
2R=$\frac{1}{2}g{t}^{2}$
x=vCt
代入数据解得 x=4m
答:(1)拉力F做了37.5J的功;
(2)经过B点后瞬间,物块对轨道的压力是30N;
(3)BD间的距离是4m.
点评 对于平抛运动的问题我们的思路是分解,从水平方向和竖直方向去研究.对于圆周运动的受力问题,关键要找出向心力的来源.

练习册系列答案
相关题目
13.某物体沿固定斜面运动,当重力对它做正功时,下列说法正确的是 ( )
| A. | 物体的重力势能一定增加,动能一定减少 | |
| B. | 物体的重力势能一定减少,动能可能不变 | |
| C. | 物体的重力势能可能增加,机械能一定不变 | |
| D. | 物体的重力势能一定减少,机械能一定不变 |
14. 如图,在一个水平方向的匀强磁场中,水平放置一粗糙的绝缘杆,在杆套有一个带正电的环,环正在沿杆运动,磁场的方向与杆的运动方向如图所示,对环在此后的运动,下列说法正确的是( )
如图,在一个水平方向的匀强磁场中,水平放置一粗糙的绝缘杆,在杆套有一个带正电的环,环正在沿杆运动,磁场的方向与杆的运动方向如图所示,对环在此后的运动,下列说法正确的是( )
 如图,在一个水平方向的匀强磁场中,水平放置一粗糙的绝缘杆,在杆套有一个带正电的环,环正在沿杆运动,磁场的方向与杆的运动方向如图所示,对环在此后的运动,下列说法正确的是( )
如图,在一个水平方向的匀强磁场中,水平放置一粗糙的绝缘杆,在杆套有一个带正电的环,环正在沿杆运动,磁场的方向与杆的运动方向如图所示,对环在此后的运动,下列说法正确的是( )| A. | 环一定做减速运动,且最终速度一定为零 | |
| B. | 环可能开始减速运动,然后做匀速运动 | |
| C. | 若环的动能发生了变化,可能是磁场力对环做了功 | |
| D. | 若环的动能发生了变化,环一定克服摩擦力做了功 |
18.关于原子模型,下列说法错误的是( )
| A. | 汤姆生发现电子,表明原子具有核式结构 | |
| B. | 卢瑟福完成的α粒子散射实验,说明了原子的“枣糕”模型是不正确的 | |
| C. | 按照玻尔理论,氢原子核外电子从高能级向低能级跃迁时,辐射出光子 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子总能量增加 |
8.洛伦兹力演示仪是由励磁线圈(也叫亥姆霍兹线圈)、洛伦兹力管和电源控制部分组成的.励磁线圈是一对彼此平行的共轴串联的圆形线圈,它能够在两线圈之间产生匀强磁场.洛伦兹力管的圆球形玻璃泡内有电子枪,能够连续发射出电子,玻璃泡内充有稀薄的气体,电子束通过泡内气体时能够显示出电子运动的径迹,其结构如图所示.若电子枪垂直磁场方向发射电子,给励磁线圈通电后,能看到电子束的径迹呈圆形.若只增大电子枪的加速电压或励磁线圈中的电流,下列说法正确的是( )


| A. | 只增大电子枪的加速电压,电子束的轨道半径变大,电子运动一周的时间(周期)不变 | |
| B. | 只增大电子枪的加速电压,电子束的轨道半径不变,电子运动一周的时间(周期)变短 | |
| C. | 只增大励磁线圈中的电流,电子束的轨道半径变小,电子运动一周的时间(周期)不变 | |
| D. | 只增大励磁线圈中的电流,电子束的轨道半径不变,电子运动一周的时间(周期)变长 |
15.下表是一辆电动自行车的部分技术指标,其中额定车速是指电动车满载情况下在平直道路上以额定功率匀速行驶的速度.
若该车满载时在平直道路上以额定功率行驶,且所受阻力大小恒定.(g取10m/s2)根据表中数据,下列说法正确的是( )
| 额定 车速 | 车质量 | 载重 | 电源 | 电源输 出电压 | 充电 时间 | 额定输 出功率 | 电动机额定工 作电压和电流 |
| 18km/h | 40kg | 80kg | 36V/12Ah | ≥36V | 6~8h | 180W | 36V/6A |
| A. | 该过程中,自行车电动机的热功率是216W | |
| B. | 该车所配电动机的内阻是1Ω | |
| C. | 该过程中,自行车所受阻力是车重(包括载重)的0.09倍 | |
| D. | 该过程中,当车速为3m/s时,加速度为0.2 m/s2 |
12.在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示.产生的交变电动势随时间变化的规律如图乙所示.则下列说法正确的是( )
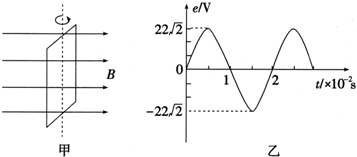

| A. | t=0.01s时穿过线框的磁通量最大 | |
| B. | 该交变电动势的有效值为11$\sqrt{2}$V | |
| C. | 该交变电动势的瞬时值表达式为e=22$\sqrt{2}$sin(100πt)V | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
14. 足够长的粗糙斜面,倾角为θ,匀强电场垂直斜面向上,一带电小球质量为m,电量为+q,从静止出发(如图),小球开始运动后,以下正确的是( )
足够长的粗糙斜面,倾角为θ,匀强电场垂直斜面向上,一带电小球质量为m,电量为+q,从静止出发(如图),小球开始运动后,以下正确的是( )
 足够长的粗糙斜面,倾角为θ,匀强电场垂直斜面向上,一带电小球质量为m,电量为+q,从静止出发(如图),小球开始运动后,以下正确的是( )
足够长的粗糙斜面,倾角为θ,匀强电场垂直斜面向上,一带电小球质量为m,电量为+q,从静止出发(如图),小球开始运动后,以下正确的是( )| A. | 小球一定沿斜面做匀加速直线运动 | |
| B. | 小球一定做匀加速直线运动,但不一定沿斜面 | |
| C. | 当E=$\frac{mgcosθ}{q}$时,小球不受斜面的摩擦力 | |
| D. | 只有Eq>mg小球就离开斜面 |
