题目内容
6. 如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )
如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )| A. | 小物块到C点后将沿斜面下滑 | |
| B. | 小物块从A点沿斜面向上滑行的最大高度为1.8m | |
| C. | 小物块与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$ | |
| D. | 推力 F的大小为4 N |
分析 由图示图象求出物块的加速度,然后应用牛顿第二定律求出动摩擦因数,根据动摩擦因数判断物块能否下滑;
根据图示图象求出物块向上滑行的最大高度;应用牛顿第二定律求出推力大小.
解答 解:A、由图乙所示图象可知,加速度:a1=$\frac{△v}{△t}$=$\frac{3}{0.9}$=$\frac{10}{3}$m/s2,a2=$\frac{△v}{△t}$=$\frac{3}{1.2-0.9}$=10m/s2,
在匀减速直线运动过程中,由牛顿第二定律知:mgsin30°+μmgcos30°=ma2,解得:μ=$\frac{\sqrt{3}}{3}$,
由于μ=tanθ=$\frac{\sqrt{3}}{3}$,物块到达C点后将静止在C点不会下滑,故A错误,C正确;
B、由图乙所示图象可知,物块向上滑行的最大距离:s=$\frac{1}{2}$×3×1.2=1.8m,向上滑行的最大高度:h=ssin30°=1.8×0.5=0.9m,故B错误;
D、在匀加速运动阶段,由牛顿第二定律得:F-mgsin30°-μmgcos30°=ma1,解得:F=4N,故D正确;
故选:CD.
点评 本题考查动力学知识与图象的综合,通过图线求出匀加速和匀减速运动的加速度是解决本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11. 在应县佛宫寺释迦塔的保护工作中,为保护倾斜木塔的安全,工作人员设法用一个垂直于天花板平面的力 F 作用在质量为m的木垫上,以支撑住倾斜的天花板,如图所示,己知天花板平面与竖直方向夹角为θ,则( )
在应县佛宫寺释迦塔的保护工作中,为保护倾斜木塔的安全,工作人员设法用一个垂直于天花板平面的力 F 作用在质量为m的木垫上,以支撑住倾斜的天花板,如图所示,己知天花板平面与竖直方向夹角为θ,则( )
 在应县佛宫寺释迦塔的保护工作中,为保护倾斜木塔的安全,工作人员设法用一个垂直于天花板平面的力 F 作用在质量为m的木垫上,以支撑住倾斜的天花板,如图所示,己知天花板平面与竖直方向夹角为θ,则( )
在应县佛宫寺释迦塔的保护工作中,为保护倾斜木塔的安全,工作人员设法用一个垂直于天花板平面的力 F 作用在质量为m的木垫上,以支撑住倾斜的天花板,如图所示,己知天花板平面与竖直方向夹角为θ,则( )| A. | 木垫可能只受到三个力的作用 | |
| B. | 木垫对天花板的弹力大小等于 F | |
| C. | 木垫对天花板的摩擦力大小等于 mgcosθ | |
| D. | 适当增大 F,天花板和木垫之间的摩擦力可能变为零 |
18. 如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
 如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )| A. | t2时刻,弹簧形变量为0 | |
| B. | t1时刻,弹簧形变量为$\frac{mgsinθ}{k}$ | |
| C. | 力F的最小值为2ma | |
| D. | A、B分离前,A、B和弹簧系统机械能增加,A和弹簧系统机械能增加 |
15.用电压表测量某段电路两端电压时,其读数为8V,如果这段电路两端电压不变,将4500Ω的电阻与电压表串联后再测其电压,结果示数为5V,则电压表内阻为( )
| A. | 1000Ω | B. | 5000Ω | C. | 7500Ω | D. | 2000Ω |
 如图所示,一电荷量q=+3×10-5C的小球,用绝缘细线悬挂于竖直放置足够大的平行金属板中的O点.电键S合上后,小球静止时细线与竖直方向的夹角θ=37°.已知两板间距d=0.1m,电源电动势E=15V,内阻r=0.5Ω,电阻R1=3Ω,R2=R3=R4=8Ω,.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求:
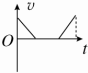
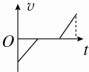
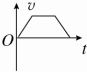
如图所示,一电荷量q=+3×10-5C的小球,用绝缘细线悬挂于竖直放置足够大的平行金属板中的O点.电键S合上后,小球静止时细线与竖直方向的夹角θ=37°.已知两板间距d=0.1m,电源电动势E=15V,内阻r=0.5Ω,电阻R1=3Ω,R2=R3=R4=8Ω,.取g=10m/s2,已知sin37°=0.6,cos37°=0.8.求: 2016年8月24日中国青年网消息,北京被称作“最能装”的8A型列车正式亮相,最大载客量达到3456人.该列车匀减速进站,停靠一段时间后又匀加速(同方向)出站,在如图所示的四个v-t图象中,正确描述了火车运动情况的是( )
2016年8月24日中国青年网消息,北京被称作“最能装”的8A型列车正式亮相,最大载客量达到3456人.该列车匀减速进站,停靠一段时间后又匀加速(同方向)出站,在如图所示的四个v-t图象中,正确描述了火车运动情况的是( )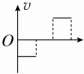
 如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:
如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:
 一重量为G=100N的物体静止在水平地面上,已知物体与水平地面之间的动摩擦因数为μ=0.25,要想把物体从静止开始移动,水平拉力必须达到30N.求:
一重量为G=100N的物体静止在水平地面上,已知物体与水平地面之间的动摩擦因数为μ=0.25,要想把物体从静止开始移动,水平拉力必须达到30N.求: