题目内容
14. 如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:
如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:(1)小球在A点处的速度大小;
(2)小球运动到最高点B时对轨道的压力.
分析 (1)球受重力、电场力、弹力,重力小于电场力,在A点,合力提供向心力,根据牛顿第二定律列式求解A点的速度大小;
(2)对从A到B过程根据动能定理列式求解B点的速度;在B点,重力、电场力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力;根据牛顿第三定律得到压力.
解答 解:(1)重力:G=mg=0.12kg×10N/kg=1.2N
电场力:F=qE=1.6×10-6C×3×106V/m=4.8N
在A点,有:qE-mg=m$\frac{{v}_{1}^{2}}{R}$
代入数据解得:v1=6m/s
(2)设球在B点的速度大小为v2,从A到B,由动能定理有:
(qE-mg)×(2R)=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
在B点,设轨道对小球弹力为FN,则有:
FN+mg-qE=$\frac{1}{2}$mv22
由牛顿第三定律有:FN′=FN
代入数据解得:FN′=21.6N
答:(1)小球在A点处的速度大小为6m/s;
(2)小球运动到最高点B时对轨道的压力为21.6N.
点评 本题关键是明确小球的受力情况和运动情况,结合动能定理和向心力公式列式分析,可以将重力和电场力合成为“等效重力”,然后就能够结合竖直平面内的圆周运动模型进行分析.

练习册系列答案
相关题目
2. 甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一路标.如图是描述两车运动的v-t图线,折线ABC和折线OBD分别描述了甲、乙两车在0~20s内的运动情况.关于甲、乙两车的运动,下列说法正确的是( )
甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一路标.如图是描述两车运动的v-t图线,折线ABC和折线OBD分别描述了甲、乙两车在0~20s内的运动情况.关于甲、乙两车的运动,下列说法正确的是( )
 甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一路标.如图是描述两车运动的v-t图线,折线ABC和折线OBD分别描述了甲、乙两车在0~20s内的运动情况.关于甲、乙两车的运动,下列说法正确的是( )
甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一路标.如图是描述两车运动的v-t图线,折线ABC和折线OBD分别描述了甲、乙两车在0~20s内的运动情况.关于甲、乙两车的运动,下列说法正确的是( )| A. | 在0~10 s内,两车逐渐靠近 | B. | 在t=10 s时,两车相遇 | ||
| C. | 在10 s~20 s内,两车逐渐远离 | D. | 在0~20 s内,两车最远距离为100 m |
19.下列粒子从传送带为零的状态经过加速电压为U的电场加速之后,哪种粒子的速度最大?(选项括号中符号的左下角标为粒子所带的电荷数,左上角标为粒子的质量数)( )
| A. | 质子(${\;}_{1}^{1}$ H) | B. | 氘核(${\;}_{1}^{2}$H) | C. | α粒子(${\;}_{2}^{4}$ He) | D. | 钠离子(${\;}_{1}^{23}$Na) |
6. 如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )
如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )
 如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )
如图甲所示,粗糙斜面与水平面的夹角为30°,质量为0.3kg的小物块静止在 A点,现有一沿斜面向上的恒定推力F作用在小物块上,作用一段时间后撤去推力 F,小物块能达到的最高位置为C点,小物块从A到 C 的 v-t 图象如图乙所示,g取10m/s2,则下列说法正确的是( )| A. | 小物块到C点后将沿斜面下滑 | |
| B. | 小物块从A点沿斜面向上滑行的最大高度为1.8m | |
| C. | 小物块与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$ | |
| D. | 推力 F的大小为4 N |
3. 如图所示,质量为m的铜棒长为L,棒的两端各与长为a的细软铜线相连,静止悬挂在磁感应强度大小为B、方向竖直向上的匀强磁场中.当棒中通过恒定电流后,铜棒向上摆动,最大偏角为θ.则棒中的电流强度为( )
如图所示,质量为m的铜棒长为L,棒的两端各与长为a的细软铜线相连,静止悬挂在磁感应强度大小为B、方向竖直向上的匀强磁场中.当棒中通过恒定电流后,铜棒向上摆动,最大偏角为θ.则棒中的电流强度为( )
 如图所示,质量为m的铜棒长为L,棒的两端各与长为a的细软铜线相连,静止悬挂在磁感应强度大小为B、方向竖直向上的匀强磁场中.当棒中通过恒定电流后,铜棒向上摆动,最大偏角为θ.则棒中的电流强度为( )
如图所示,质量为m的铜棒长为L,棒的两端各与长为a的细软铜线相连,静止悬挂在磁感应强度大小为B、方向竖直向上的匀强磁场中.当棒中通过恒定电流后,铜棒向上摆动,最大偏角为θ.则棒中的电流强度为( )| A. | I=$\frac{mg(1-cosθ)}{BLsinθ}$ | B. | I=$\frac{mg(1-sinθ)}{BLcosθ}$ | ||
| C. | I=$\frac{mgtanθ}{BL}$ | D. | I=$\frac{mg}{BLtanθ}$ |
4.如图所示,水平力F把一个物体紧压在竖直墙上,物体静止不动,则可知( )


| A. | F增大时静摩擦力变大 | B. | 静摩擦力方向竖直向上 | ||
| C. | 静摩擦力大小一定等于μF | D. | 静摩擦力大小等于μmg |
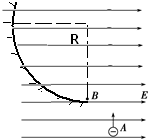 如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求:
如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求: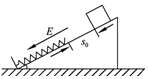 如图所示,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
如图所示,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.