题目内容
1．如图1为验证牛顿第二定律的实验装置示意图．图中打点计时器的电源为50Hz的交流电源，打点的时间间隔用△t表示．在小车质量未知的情况下，某同学设计了一种方法用来探究“在外力一定的条件下，物体的加速度与其质量间的关系”．
（1）本实验中，为了保证在改变小车中砝码的质量时，小车所受的拉力近似不变，小吊盘和盘中物块的质量之和应满足的条件是远小于小车和砝码的总质量．
（2）图2是实验所得纸带，设纸带上三个相邻计数点的间距为s1、s2和s3．a可用s1、s3和△t表示为a=$\frac{{s}_{3}-{s}_{1}}{50（△t）^{2}}$．
图为用米尺测量某一纸带上的s1、s3的情况，由图可读出s1=24.0mm，s3=47.0mm，由此求得加速度的大小a=1.15m/s2（保留三位有效数字）．
分析 （1）当根据盘及盘中物块的质量远小于小车总质量时可以近似认为小车受到的拉力等于盘及盘中重物的重力，实验注意事项分析答题；
（2）由图示刻度尺读出其示数；应用匀变速运动的推论求出加速度．
解答 解：（1）探究牛顿第二定律实验时，当小吊盘和盘中物块的质量之和远小于小车和车中砝码的总质量时，可以近似认为小车受到的拉力等于小吊盘和盘中物块受到的重力，认为小车受到的拉力不变．
（2）由图示纸带可知，计数点间的时间间隔：t=5△t，由匀变速直线运动的推论：△x=at2可知加速度为：a=$\frac{{s}_{3}-{s}_{1}}{2{t}^{2}}$=$\frac{{s}_{3}-{s}_{1}}{50（△t）^{2}}$；
由图示刻度尺可知：s1=3.65-1.25=2.40cm=0.0240m=24.0mm，s3=12.0-7.30=4.70cm=0.0470m=47.0mm，
由图示纸带可知：△t=0.02×5=0.1s，加速度为：a=$\frac{{s}_{3}-{s}_{1}}{2{t}^{2}}$=$\frac{0.0470-0.0240}{2×0．{1}^{2}}$=1.15m/s2；
故答案为：（1）远小于小车和砝码的总质量；（2）$\frac{{s}_{3}-{s}_{1}}{50（△t）^{2}}$；24.0；47.0；1.15．
点评 本题考查了实验注意事项、刻度尺读数、求加速度，知道实验注意事项、实验原理、应用匀变速直线运动的推论即可正确解题．对刻度尺读数时要注意刻度尺的分度值，要注意估读一位．
练习册系列答案
相关题目
如图所示，在竖直放置的足够大的铅屏A的右表面上贴着β 射线（即电子）放射源P，已知射线实质为高速电子流，放射源放出β 粒子的速度为v0．足够大的荧光屏M与铅屏A平行放置，相距为d，其间有水平向左的匀强电场，电场强度大小为E．已知电子电量为e，电子质量为m．求：
如图所示，竖直平面直角坐标系中，一半径为R的绝缘光滑管道位于其中，管道圆心坐标为（0，R），其下端点与x轴相切与坐标原点，其上端点与y轴交于C点，坐标为（0，2R）．在第二象限内，存在水平向右、范围足够大的匀强电场，电场强度大小为E1=$\frac{\sqrt{3}mg}{3q}$，在x≥R，y≥0范围内，有水平向左，范围足够大的匀强电场，电场强度大小为E1=$\frac{mg}{q}$．现有一与x轴正方向夹角为45°，足够长的绝缘斜面位于第一象限的电场中，斜面底端坐标为（R，0），x轴上0≤x≤R范围内是水平光滑轨道，左端与管道下端相切，右端与斜面底端平滑连接，有一质量为m，带电量为+q的小球，从静止开始，由斜面上某点A下滑，通过水平光滑轨道（不计转角处能量损失），从管道下端点B进入管道（小球直径略小于管道内径，不计小球的电量损失）（已知重力加速度为g）．试求：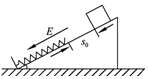
如图所示，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中．一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态．一质量为m、带电量为q（q＞0）的滑块从距离弹簧上端为s0处静止释放，滑块在运动过程中电量保持不变，设滑块与弹簧接触过程没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g．
如图所示，两块竖直放置的平行金属板A、B，板距d=0.4m，两板间的电压U=400V，板间有一匀强电场．在A、B两板上端连线的中点Q的正上方，距Q为h=1.25m的P点处有一带正电的小球，已知小球的质量m=5×10-6 kg，电荷量q=5×10-8 C．设A、B板足够长，g取10m/s2．试求：
6．
如图甲所示，粗糙斜面与水平面的夹角为30°，质量为0.3kg的小物块静止在 A点，现有一沿斜面向上的恒定推力F作用在小物块上，作用一段时间后撤去推力 F，小物块能达到的最高位置为C点，小物块从A到 C 的 v-t 图象如图乙所示，g取10m/s2，则下列说法正确的是（ ）
如图甲所示，粗糙斜面与水平面的夹角为30°，质量为0.3kg的小物块静止在 A点，现有一沿斜面向上的恒定推力F作用在小物块上，作用一段时间后撤去推力 F，小物块能达到的最高位置为C点，小物块从A到 C 的 v-t 图象如图乙所示，g取10m/s2，则下列说法正确的是（ ）| A． | 小物块到C点后将沿斜面下滑 | |
| B． | 小物块从A点沿斜面向上滑行的最大高度为1.8m | |
| C． | 小物块与斜面间的动摩擦因数为$\frac{\sqrt{3}}{3}$ | |
| D． | 推力 F的大小为4 N |
13．有两个共点力，一个力的大小是5N，另一个力的大小是2N，它们合力的大小可能是（ ）
| A． | 10 N | B． | 7 N | C． | 5 N | D． | 2N |
在如图示的电路中，
为一电动机，调节滑动变阻器，当电动机恰好正常工作时，电流表
示数为1A，电压表V1示数为6V，电压表V2示数为8V．已知所有的电表均为理想电表，电源内阻r=1Ω，电动机线圈的电阻rM=2Ω．求：
物体A重20N，物体B重100N，B与水平面间的动摩擦因数为0.3．各物都处于如图所示的静止状态．求：