题目内容
16.如图甲所示,直角坐标系xoy的第二象限有一半径为R=a的圆形区域,圆形区域的圆心O1坐标为(-a,a),与坐标轴分别相切于P点和N点,整个圆形区域内分布有磁感应强度大小为B的匀强磁场,其方向垂直纸面向里(图中未画出).带电粒子以相同的速度在纸面内从P点进入圆形磁场区域,速度方向与x轴负方向成θ角,当粒子经过y轴上的M点时,速度方向沿x轴正方向,已知M点坐标为(0,$\frac{4a}{3}$).带电粒子质量为m、带电量为-q.忽略带电粒子间的相互作用力,不计带电粒子的重力,求:
(1)带电粒子速度v大小和cosθ值;
(2)若带电粒子从M点射入第一象限,第一象限分布着垂直纸面向里的匀强磁场,已知带电粒子在该磁场的一直作用下经过了x轴上的Q点,Q点坐标为(a,0),该磁场的磁感应强度B′大小为多大?
(3)若第一象限只在y轴与直线x=a之间的整个区域内有匀强磁场,磁感应强度大小仍为B.方向垂直纸面,磁感应强度B随时间t变化(B-t图)的规律如图乙所示,已知在t=0时刻磁感应强度方向垂直纸面向外,此时某带电粒子刚好从M点射入第一象限,最终从直线x=a边界上的K点(图中未画出)穿出磁场,穿出磁场时其速度方向沿x轴正方向(该粒子始终只在第一象限内运动),则K点到x轴最大距离为多少?要达到此最大距离,图乙中的T值为多少?
分析 (1)带电粒子在圆形磁场区域中做圆周运动,确定出圆心和半径,由洛伦兹力等于向心力,列式求得v的大小.由几何关系求解cosθ值;
(2)带电粒子以平行于x轴正方向的速度从M点进入磁场区域中做圆周运动,根据几何知识求出轨迹半径,即可由牛顿第二定律求解B.
(3)画出粒子运动的轨迹,由几何知识求解K点到x轴最大距离.根据轨迹的圆心角求解图乙中的T值.
解答 解:(1)带电粒子在圆形磁场区域中做圆周运动的圆心为O2,离开圆形磁场区域
时的位置为H,连接PO1HO2可知,该四边形为菱形,带电粒子做圆周运动的半径:
r=a
由于qvB=m$\frac{{v}^{2}}{r}$
得:v=$\frac{qBa}{m}$
由于PO1在竖直方向,半径HO2也为竖直方向,由图可知:
r+rcosθ=$\frac{4}{3}$a
解得:cosθ=$\frac{1}{3}$
(2)由图可知,带电粒子以平行于x轴正方向的速度从M点进入磁场区域中做圆周运
动,设半径为r3,由几何关系有:
tanβ=$\frac{a}{\frac{4}{3}a}$=$\frac{3}{4}$,β=37°
则:cosβ=$\frac{\frac{1}{2}MQ}{{r}_{3}}$=$\frac{\frac{5}{6}a}{{r}_{3}}$
得:r3=$\frac{25}{24}$a
而r3=$\frac{mv}{qB′}$
得:B′=$\frac{24}{25}$B
(3)由图知:圆O4与直线x=a相切于C点,圆
O5与y轴相切于D点,两圆弧相切于E点,带电粒子运动到K点时离x轴距离最大,
O4 O5=2r=2a
cos∅=$\frac{1}{2}$,∅=60°
最大距离KQ=$\frac{4a}{3}$+3r+2rsinΦ=($\frac{10}{3}$+$\sqrt{3}$)a
带电粒子运动周期T0=$\frac{2πm}{qB}$
由$\frac{1}{2}$T=$\frac{150°}{360°}$×T0
解得 T=$\frac{5πm}{3qB}$
答:
(1)带电粒子速度v大小为$\frac{qBa}{m}$,cosθ值是$\frac{1}{3}$;
(2)该磁场的磁感应强度B′大小为$\frac{24}{25}$B.
(3)K点到x轴最大距离为($\frac{10}{3}$+$\sqrt{3}$)a,要达到此最大距离,图乙中的T值为$\frac{5πm}{3qB}$.
点评 本题关键是明确粒子的受力情况和运动规律,画出临界轨迹,结合牛顿第二定律和几何关系分析解答.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )
如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )| A. | 8cm | B. | 3cm | C. | 5cm | D. | 11cm |
 某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )
某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )| A. | A点的电场强度大于B点的电场强度 | |
| B. | 将正电荷从A点移到C点,电势能增加 | |
| C. | A点的电势高于B点的电势 | |
| D. | 将负电荷从A点移到B点,电场力做正功 |
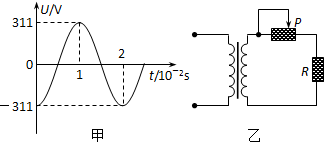
| A. | 副线圈输出电压的频率为100Hz | |
| B. | 副线圈输出电压的有效值为5V | |
| C. | P向左移动时,变压器原、副线圈的电流都减小 | |
| D. | P向左移动时,变压器的输入功率增加 |
| A. | 卢瑟福提出原子的核式结构模型建立的基础是α粒子的散射实验 | |
| B. | 发现天然放射现象的意义在于使人类认识到原子核具有复杂的结构 | |
| C. | 在用气垫导轨和光电门传感器做验证动量守恒定律的实验中,在两滑块相碰的端面上装不装上弹性碰撞架,不会影响动量是否守恒 | |
| D. | 原子核内的某一核子与其他核子间都有核力作用 | |
| E. | 氢原子的核外电子,在由离核较远的轨道自发跃迁到离核较近的轨道的过程中,放出光子,电子动能增加,原子的电势能增加 |
 在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时( )
在汽车无极变速器中,存在如图所示的装置,A是与B同轴相连的齿轮,C是与D同轴相连的齿轮,A、C、M为相互咬合的齿轮.已知齿轮A、C规格相同,半径为R,齿轮B、D规格也相同,半径为1.5R,齿轮M的半径为0.9R.当齿轮M如图方向转动时( )| A. | 齿轮D和齿轮B的转动方向相同 | |
| B. | 齿轮D和齿轮A的转动周期之比为1:1 | |
| C. | 齿轮M和齿轮C的角速度大小之比为9:10 | |
| D. | 齿轮M和齿轮B边缘某点的线速度大小之比为2:3 |
 某待测电阻RX的阻值大约为100Ω,现要测量其阻值,实验室提供有如下器材:
某待测电阻RX的阻值大约为100Ω,现要测量其阻值,实验室提供有如下器材: 如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了h.已知大气压强为p0.重力加速度为g,不计活塞与气缸间摩擦.
如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了h.已知大气压强为p0.重力加速度为g,不计活塞与气缸间摩擦.