题目内容
13. 如图所示,用一长为L的细线吊着一个质量为m、电量为+q的小球,整个装置放在磁感应强度为B,方向垂直纸面向外的匀强磁场中.将细线拉到水平位置,由静止释放小球.求:小球第一次到达最低点时的速度大小和此时细线对小球的拉力大小.
如图所示,用一长为L的细线吊着一个质量为m、电量为+q的小球,整个装置放在磁感应强度为B,方向垂直纸面向外的匀强磁场中.将细线拉到水平位置,由静止释放小球.求:小球第一次到达最低点时的速度大小和此时细线对小球的拉力大小.
分析 (1)根据动能定理,结合牛顿第二定律与左手定则,即可求解;
(2)牛顿第二定律,结合向心力表达式,即可求解.
解答 解:小球第一次到达最低点的过程中只有重力做功,设速度为v,则由动能定理可得:mgL=$\frac{1}{2}$mv2
得:v=$\sqrt{2gL}$
由左手定则可得,小球第一次到达最低点时受到的洛伦兹力的方向向上,在最低点根据牛顿第二定律得:
F+Bqv-mg=m$\frac{{V}^{2}}{L}$
解得:F=3mg-Bq$\sqrt{2gL}$
答:小球运动到最低点的速度大小是$\sqrt{2gL}$;小球第一次到达最低点时受到的细线的拉力的大小3mg-Bq$\sqrt{2gL}$.
点评 考查牛顿第二定律、动能定律的应用,掌握左手定则与右手定则的区别,注意运用动能定理时对过程的选取.

练习册系列答案
相关题目
3. 如图所示,在纸面内两条竖直直线之间存在匀强磁场,磁场方向垂直纸面向里.两个带电粒子a和b以相同的动能同时从A点出发,恰好在水平连线上的B点相遇(A和B是磁场边界上的两点),已知a和b的初始速度与AB连线夹角分别为60°和30°,不计重力.下列说法正确的是( )
如图所示,在纸面内两条竖直直线之间存在匀强磁场,磁场方向垂直纸面向里.两个带电粒子a和b以相同的动能同时从A点出发,恰好在水平连线上的B点相遇(A和B是磁场边界上的两点),已知a和b的初始速度与AB连线夹角分别为60°和30°,不计重力.下列说法正确的是( )
 如图所示,在纸面内两条竖直直线之间存在匀强磁场,磁场方向垂直纸面向里.两个带电粒子a和b以相同的动能同时从A点出发,恰好在水平连线上的B点相遇(A和B是磁场边界上的两点),已知a和b的初始速度与AB连线夹角分别为60°和30°,不计重力.下列说法正确的是( )
如图所示,在纸面内两条竖直直线之间存在匀强磁场,磁场方向垂直纸面向里.两个带电粒子a和b以相同的动能同时从A点出发,恰好在水平连线上的B点相遇(A和B是磁场边界上的两点),已知a和b的初始速度与AB连线夹角分别为60°和30°,不计重力.下列说法正确的是( )| A. | a粒子带正电荷,b粒子带负电荷 | B. | a粒子带负电荷,b粒子带正电荷 | ||
| C. | a和b的质量之比为1:2 | D. | a和b的质量之比为3:4 |
1. 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,则( )
 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,则( )| A. | x2=5x1 | B. | x2=9x1 | C. | v2=3v1 | D. | v2=5v1 |
18.用10N的力拉原长为20cm的弹簧,长度变为25cm,则这根弹簧的劲度系数为( )
| A. | 400N/m | B. | 200N/m | C. | 80N/m | D. | 40N/m |
5.在以5米/秒2的加速度加速下降的电梯里,有一个秤,秤上放60千克的物体,(g取10米/秒2)则( )
| A. | 物体处于超重状态 | B. | 物体处于失重状态 | ||
| C. | 秤的示数为300N | D. | 秤的示数为900N |
3.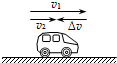 如图所示,汽车向右沿直线运动,原来的速度是v1,经过一小段时间之后,速度变为v2,△v表示速度的变化量.由图中所示信息可知( )
如图所示,汽车向右沿直线运动,原来的速度是v1,经过一小段时间之后,速度变为v2,△v表示速度的变化量.由图中所示信息可知( )
 如图所示,汽车向右沿直线运动,原来的速度是v1,经过一小段时间之后,速度变为v2,△v表示速度的变化量.由图中所示信息可知( )
如图所示,汽车向右沿直线运动,原来的速度是v1,经过一小段时间之后,速度变为v2,△v表示速度的变化量.由图中所示信息可知( )| A. | 汽车在做加速直线运动 | B. | 汽车的加速度方向与v1的方向相同 | ||
| C. | 汽车的加速度方向与△v的方向相同 | D. | 汽车的加速度方向与△v的方向相反 |
 质检员要精确地检测某产品中一个槽的深度,他应从下列器材中选取B(填代号)进行测量.
质检员要精确地检测某产品中一个槽的深度,他应从下列器材中选取B(填代号)进行测量. 一个质量为4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.(g=10m/s2)求
一个质量为4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.(g=10m/s2)求 如图所示,轻绳一端系在质量为mA=30kg的物体A上,另一端系在一个质量为m=2kg套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点,使物体A从如图所示实线位置O缓慢下降到虚线位置O′,此时θ=53°,圆环恰好要下滑,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,轻绳一端系在质量为mA=30kg的物体A上,另一端系在一个质量为m=2kg套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点,使物体A从如图所示实线位置O缓慢下降到虚线位置O′,此时θ=53°,圆环恰好要下滑,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: