Question

如图所示，靠摩擦传动做匀速转动的大小两轮接触面相互不打滑，大轮的半径是小轮半径的两倍．A、B分别为大小轮边缘上的点，C为大轮上一条半径的中点，则下列关系正确的是（ ）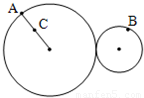

A．v_B：v_C=2：1
B．a_A：a_B=2：1
C．a_A：a_C=2：1
D．a_B：a_C=2：1

Answer 1

【答案】分析：在转盘问题中要明确转盘接触的边缘线速度大小相同，同一转盘上角速度相同，然后利用角速度、线速度、半径之间的关系以及向心加速度公式进行求解．
解答：解：根据转盘转动特点可知：v_A=v_B，ω_A=ω_C  ①
向心加速度公式为：a=ω²r    ②
由图知半径关系为：r_A=2r_C，r_B=r_C ③
由①②③联立可解得：v_B=v_C=2：1，a_A：a_B=1：2，a_A：a_C=2：1，a_B：a_C=4：1，故BCD错误，A正确．
故选A．
点评：本题借助于转盘考察了角速度、线速度、半径之间的关系以及向心加速度公式的应用，理论联系实际，加强了知识在生活中的应用．