题目内容
18.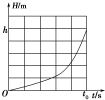 万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.
万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.| A. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| B. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| C. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 | |
| D. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 |
分析 由图示图象求出物体下落的位移与所用是时间,然后由匀加速直线运动的位移公式求出重力加速度;
卫星绕星球表面做圆周运动,万有引力提供向心力,由牛顿第二定律可以求出水平抛出的速度;
将物体竖直上抛时,卫星机械能守恒,由机械能守恒定律可以求出竖直上抛的速度.
解答 解:物体自由下落,物体做自由落体运动,由图示图象可知,物体位移为h时所用时间为t0,由自由落体运动的位移公式得:h=$\frac{1}{2}$gt02,解得:g=$\frac{2h}{{t}_{0}^{2}}$;
A、物体绕星球表面做圆周运动,万有引力提供向心力,由牛顿第二定律得:m$\frac{{v}^{2}}{R}$=mg,解得:v=$\frac{1}{{t}_{0}}$$\sqrt{2hR}$,当水平抛出物体的速度大于等于$\frac{1}{{t}_{0}}$$\sqrt{2hR}$时,物体将不会再返回地面,故AB正确;
C、抛出物体过程时,物体机械能守恒,设发射速度为v′,卫星绕星球表面运动时,由机械能守恒定律得:
-$\frac{GMm}{R}$+$\frac{1}{2}$mv′2=0+0,万有引力等于重力:$\frac{GMm′}{{R}^{2}}$=m′g,解得:v′=$\frac{2}{{t}_{0}}$$\sqrt{Rh}$,故C错误,D正确;
故选:ABD.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力,能读懂题给予的信息是解题的前提,应用万有引力公式、牛顿第二定律与机械能守恒定律可以解题.

练习册系列答案
相关题目
9.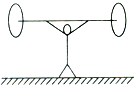 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )| A. | 750 N | B. | 800 N | C. | 1000 N | D. | 1200 N |
3.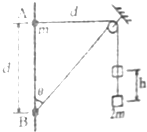 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\frac{d}{2}$ | |
| B. | 环到达B处时,环与重物的速度大小相等 | |
| C. | 环从A到B,环减少的机械能大于重物增加的机械能 | |
| D. | 环能下降的最大高度为$\frac{4d}{3}$ |
10.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上,其中L远大于R.已知万有引力常量为G.忽略星体自转效应,关于四星系统,下列说法正确的是( )
| A. | 四颗星圆周运动的轨道半径均为$\frac{L}{2}$ | |
| B. | 四颗星圆周运动的线速度均为 $\sqrt{\frac{Gm}{L}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星圆周运动的周期均为2π $\sqrt{\frac{2{L}^{3}}{(4+\sqrt{2})Gm}}$ | |
| D. | 四颗星表面的重力加速度均为G$\frac{m}{{R}^{2}}$ |
8.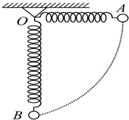 如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
 如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )| A. | 小球做圆周运动 | B. | 弹簧弹性势能不变 | ||
| C. | 小球的机械能减少 | D. | 小球和弹簧组成的系统机械能减少 |

 如图所示,n块厚度为d的相同的砖块,靠在一起平放在地面上.今将它们一块一块向上叠起来,这堆砖的重心升高了多少?
如图所示,n块厚度为d的相同的砖块,靠在一起平放在地面上.今将它们一块一块向上叠起来,这堆砖的重心升高了多少?
 在“研究平抛运动”实验中:
在“研究平抛运动”实验中: