题目内容
10.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上,其中L远大于R.已知万有引力常量为G.忽略星体自转效应,关于四星系统,下列说法正确的是( )| A. | 四颗星圆周运动的轨道半径均为$\frac{L}{2}$ | |
| B. | 四颗星圆周运动的线速度均为 $\sqrt{\frac{Gm}{L}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星圆周运动的周期均为2π $\sqrt{\frac{2{L}^{3}}{(4+\sqrt{2})Gm}}$ | |
| D. | 四颗星表面的重力加速度均为G$\frac{m}{{R}^{2}}$ |
分析 在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力,根据合力提供向心力,求出星体匀速圆周运动的线速度和周期.
根据万有引力等于重力,求出星体表面的重力加速度.
解答 解:A、任一颗星体在其他三个星体的万有引力作用下,合力方向指向对角线的交点,围绕正方形对角线的交点做匀速圆周运动,任一星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,轨道半径均:r=$\frac{\sqrt{2}}{2}$L,故A错误.
B、星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:G$\frac{{m}^{2}}{(\sqrt{2}L)^{2}}$+G$\frac{{m}^{2}}{{L}^{2}}$cos45°=m$\frac{{v}^{2}}{\frac{\sqrt{2}}{2}L}$,解得:v=$\sqrt{\frac{(4+\sqrt{2})Gm}{4L}}$,故B错误;
C、由牛顿第二定律得:G$\frac{{m}^{2}}{(\sqrt{2}L)^{2}}$+G$\frac{{m}^{2}}{{L}^{2}}$cos45°=m$(\frac{2π}{T})^{2}$•$\frac{\sqrt{2}L}{2}$,解得:T=2π$\sqrt{\frac{2{L}^{3}}{(4+\sqrt{2})Gm}}$,故C正确;
D、星球表面的物体受到的万有引力等于它受到的重力,即:G$\frac{mm′}{{R}^{2}}$=m′g,解得:g=$\frac{Gm}{{R}^{2}}$,故D正确;
故选:CD.
点评 本题考查了万有引力定律的应用,解决本题的关键掌握万有引力等于重力,以及知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.

| A. | mg,mg | B. | $\frac{mg}{2}$,$\frac{mg}{2}$ | C. | $\frac{mg}{2}$,mg | D. | mg,$\frac{mg}{2}$ |
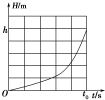 万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.
万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.| A. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| B. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| C. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 | |
| D. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 |
| A. | 重力势能有正、负值,表示物体的重力势能是矢量 | |
| B. | 只要物体在水平面以下,其重力势能为负值 | |
| C. | 卫星绕地球做椭圆运动,当由近地点向远地点运动时,其重力势能减小 | |
| D. | 重力势能是地球与物体所组成的系统共有的 |
| A. | 电容器板间场强为$\frac{U}{d}$,电压增为2U | |
| B. | 电容器板间场强为$\frac{U}{2d}$,电压仍为U | |
| C. | 电容器电容增大为2C,电量增加为2CU | |
| D. | 电容器电容减小为$\frac{C}{2}$,电量为CU |
 距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )
距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )| A. | 1.25 m | B. | 2.25 m | C. | 3.75 m | D. | 4.75 m |
| A. | 元电荷实质上是指电子和质子本身 | |
| B. | 所有带电体的电荷量一定等于元电荷的整数倍 | |
| C. | 物体所带电荷量可以是任意值 | |
| D. | 元电荷e的值最早是由美国科学家富兰克林通过实验测定的 |
