题目内容
3.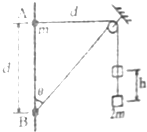 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\frac{d}{2}$ | |
| B. | 环到达B处时,环与重物的速度大小相等 | |
| C. | 环从A到B,环减少的机械能大于重物增加的机械能 | |
| D. | 环能下降的最大高度为$\frac{4d}{3}$ |
分析 环刚开始释放时,重物由静止开始加速.根据数学几何关系求出环到达B处时,重物上升的高度.对B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,从而求出环在B处速度与重物的速度之比.环和重物组成的系统机械能是守恒的.
解答 解:A、根据几何关系有,环从A下滑至B点时,下降的高度为d,则重物上升的高度为:h=$\sqrt{2}$d-d=($\sqrt{2}$-1)d,故A错误;
B、环到达B处时,对环B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,有:v环cos45°=v物,所以有v环=$\sqrt{2}$v物,故B错误;
C、环下滑过程中无摩擦力做功,故系统机械能守恒,即有环减小的机械能等于重物增加的机械能,故C错误;
D、设环下滑到最大高度为h时环和重物的速度均为0,此时重物上升的最大高度为$\sqrt{{h}^{2}+{d}^{2}}$-d,根据系统的机械能守恒有:mgh=2mg($\sqrt{{h}^{2}+{d}^{2}}$-d )
解得:h=$\frac{4d}{3}$,故D正确.
故选:D
点评 解决本题的关键知道系统机械能守恒,知道环沿绳子方向的分速度的等于重物的速度.要注意环下降的高度和重物上升的高度是不等,应根据几何知识求解.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
11.关于力学单位制说法中正确的是( )
| A. | 在国际单位制中,质量的基本单位是kg,也可以是g | |
| B. | kg、m、J是基本单位 | |
| C. | kg、m/s、N是导出单位 | |
| D. | 只有在国际单位制中,牛顿第二定律的表达式才是F=ma |
18.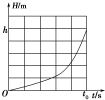 万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.
万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.
 万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.
万有引力作用下的物体具有引力势能,取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量,M、m分别为星球和物体的质量),在一半径为R的星球上,一物体从星球表面某高度处自由下落(不计空气阻力),自开始下落计时,得到物体离星球表面高度H随时间t变化的图象如图7所示,则( )°.| A. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| B. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度水平抛出一物体,物体将不再落回星球表面 | |
| C. | 在该星球表面上以$\frac{1}{t0}$$\sqrt{2hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 | |
| D. | 在该星球表面上以$\frac{2}{t0}$$\sqrt{hR}$的初速度竖直上抛一物体,物体将不再落回星球表面 |
8. 有一系列斜面,倾角各不相同,它们的顶端都在O点,如图所示.有一系列完全相同的滑块(可视为质点)从O点同时由静止释放,分别到达各斜面上的A、B、C、D…各点,下列判断正确的是( )
有一系列斜面,倾角各不相同,它们的顶端都在O点,如图所示.有一系列完全相同的滑块(可视为质点)从O点同时由静止释放,分别到达各斜面上的A、B、C、D…各点,下列判断正确的是( )
 有一系列斜面,倾角各不相同,它们的顶端都在O点,如图所示.有一系列完全相同的滑块(可视为质点)从O点同时由静止释放,分别到达各斜面上的A、B、C、D…各点,下列判断正确的是( )
有一系列斜面,倾角各不相同,它们的顶端都在O点,如图所示.有一系列完全相同的滑块(可视为质点)从O点同时由静止释放,分别到达各斜面上的A、B、C、D…各点,下列判断正确的是( )| A. | 若各斜面光滑,且这些滑块到达A、B、C、D…各点的速率相同,则A、B、C、D…各点处在同一水平线上 | |
| B. | 若各斜面光滑,且这些滑块到达A、B、C、D…各点的速率相同,则A、B、C、D…各点处在同一竖直线上 | |
| C. | 若各斜面光滑,且这些滑块到达A、B、C、D…各点的时间相同,则A、B、C、D…各点处在同一竖直面内的圆周上 | |
| D. | 若各斜面与这些滑块间有相同的摩擦因数,且到达A、B、C、D…各点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一竖直线上 |
15.平行板电容器电容为C,充电到电压为U后断开电源,然后把两极板间距离由d增大到2d,则( )
| A. | 电容器板间场强为$\frac{U}{d}$,电压增为2U | |
| B. | 电容器板间场强为$\frac{U}{2d}$,电压仍为U | |
| C. | 电容器电容增大为2C,电量增加为2CU | |
| D. | 电容器电容减小为$\frac{C}{2}$,电量为CU |
12.已成为我国首个人造太阳系小行星的嫦娥二号卫星,2014年2月再次刷新我国深空探测最远距离纪录,超过7000万公里.嫦娥二号是我国探月工程二期的先导星,它先在距月球表面高度为h的轨道上做匀速圆周运动,运行周期为T;然后从月球轨道出发飞赴日地拉格朗日L 2点进行科学探测.若以R表示月球的半径,引力常量为G,则( )
| A. | 嫦娥二号卫星绕月运行时的线速度为$\frac{2π(R+r)}{T}$ | |
| B. | 月球的质量为$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$ | |
| C. | 物体在月球表面自由下落的加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| D. | 嫦娥二号卫星在月球轨道经过减速才能飞赴拉格朗日L2点 |
 在测定金属的电阻率的实验中,其实验步骤如下:
在测定金属的电阻率的实验中,其实验步骤如下: