题目内容
13.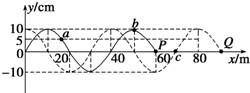 一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )| A. | 这列波的波速可能为50m/s | |
| B. | 从t+0.6 s时刻开始,经过0.5T,质点b沿x轴正方向运动20m | |
| C. | 质点c在这段时间内通过的路程可能为60 cm | |
| D. | 若T=0.8s,则当t+0.5s时刻,质点b、P的位移相同 | |
| E. | 若T=0.8s,当t+0.4s时刻开始计时,则质点c的振动方程为y=0.1sin($\frac{5}{2}$πt)(m) |
分析 由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式;由波速可知周期的表达式,则可得出质点的路程及位移及质点的振动方程.
解答 解:A、由图可知,波的波长为40m;两列波相距0.6s=(n+$\frac{3}{4}$)T,故周期T=$\frac{2.4}{4n+3}$; 波速v=$\frac{λ}{T}=\frac{40}{2.4}(4n+3)$m/s=$\frac{50}{3}$m/s,(n=0,1,2,…) 当n=0时,当v=50m/s时,故A正确;
B、质点只能上下振动,不能随波迁移,所以质点b不能沿x轴正方向运动,故B错误;
C、c的路程为60cm说明c振动了1.5个周期,则可有:$\frac{10}{v}$+1.5T=0.6,即$\frac{3}{5(4n+3)}+\frac{3.6}{4n+3}$=0.6,解得,n=1时满足条件,故C正确;
D、在 t 时刻,因波沿X轴正方向传播,所以此时质点P是向上振动的,经0.5秒后,P是正在向下振动(负位移),是经过平衡位置后向下运动0.1秒;而质点b是正在向上振动的(负位移),是到达最低点后向上运动0.1秒,因为0.2秒等于$\frac{T}{4}$,可见此时两个质点的位移是相同的. 故D正确;
E、当T=0.8s,当t+0.4s时刻时,质点c在上端最大位移处,据ω=$\frac{2π}{T}=\frac{2π}{0.8}$rad/s=$\frac{5}{2}$rad/s,据图知A=0.1m,当从t+0.4s时刻时开始计时,则质点c的振动方程为x=0.1cos($\frac{5}{2}$πt)(m),故E错误.
故选:ACD
点评 本题考查对波动图象的理解能力.知道两个时刻的波形时,往往应用波形的平移法来理解.

| A. | 天然放射现象说明原子核内部具有复杂的结构 | |
| B. | α粒子散射实验说明原子核内部具有复杂的结构 | |
| C. | 原子核发生β衰变生成的新核原子序数增加 | |
| D. | 氢原子从能级3跃迁到能级2辐射出的光子的波长小于从能级2跃迁到能级1辐射出的光子的波长 | |
| E. | γ射线是原子核内部发生核反应而释放出的多余的能量 |
| A. | 由于同步卫星相对地面静止,所以同步卫星处于平衡状态 | |
| B. | 由ω=$\frac{v}{r}$可知,在保证角速度和地球自转角速度相同的情况下,人类可通过调节同步卫星的线速度来调节同步卫星的高度 | |
| C. | 同步卫星的加速度比静止在赤道上的物体随地球自转的加速度大 | |
| D. | 若同步卫星的高度是地球半径的n倍,则同步卫星的线速度是第一宇宙速度的$\sqrt{\frac{1}{n}}$ |
 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )| A. | R=R0$\root{3}{\frac{{{t}_{0}}^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | B. | R=R0$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$ | ||
| C. | R=R0$\root{3}{\frac{({t}_{0}+{T}_{0})^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | D. | R=R0$\root{3}{\frac{{t}_{0}}{{t}_{0}-{T}_{0}}}$ |
 如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )
如图所示,质量M=2kg、长L=2m的长木板静止放置在光滑水平面上,在其左端放置一质量m=1kg的小木块(可视为质点).先相对静止,然后用一水平向右、F=4N的力作用在小木块上,经过时间t=2s,小木块从长木板另一端滑出,取g=10m/s2,则( )| A. | 小木块与长木板之间的动摩擦因数为0.1 | |
| B. | 在整个运动过程中由于摩擦产生的热量为8J | |
| C. | 小木块脱离长木板的瞬间,拉力F的功率为16W | |
| D. | 长木板在运动过程中获得的机械能为16J |
 “神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )
“神舟十号”与“天宫一号”已5次成功实现交会对接.如图所示,交会对接前“神舟十号”飞船先在较低圆轨道1上运动,在适当位置经变轨与在圆轨道2上运动的“天宫一号”对接.M、Q两点在轨道1上,P点在轨道2上,三点连线过地球球心,把飞船的加速过程简化为只做一次短时加速.下列关于“神舟十号”变轨过程的描述,正确的有( )| A. | “神舟十号”在M点加速,可以在P点与“天宫一号”相遇 | |
| B. | “神舟十号”在M点经一次加速,即可变轨到轨道2 | |
| C. | “神舟十号”经变轨后速度总大于变轨前的速度 | |
| D. | “神舟十号”变轨后的运行周期总小于变轨前的运行周期 |
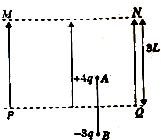 如图所示,在真空中的竖直平面内,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B,A球的电荷量为+4q,B球的电荷量为-3q,组成一带电系统.虚线MN与PQ平行,开始时PQ恰为杆的中垂线.在MN与PQ间加竖直向上的匀强电场,恰能使带电系统静止不动.现使电场强度突然加倍(已知当地重力加速度为g),求:
如图所示,在真空中的竖直平面内,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B,A球的电荷量为+4q,B球的电荷量为-3q,组成一带电系统.虚线MN与PQ平行,开始时PQ恰为杆的中垂线.在MN与PQ间加竖直向上的匀强电场,恰能使带电系统静止不动.现使电场强度突然加倍(已知当地重力加速度为g),求: