题目内容
8. 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )
经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B运动轨道半径R( )| A. | R=R0$\root{3}{\frac{{{t}_{0}}^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | B. | R=R0$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$ | ||
| C. | R=R0$\root{3}{\frac{({t}_{0}+{T}_{0})^{2}}{({t}_{0}-{T}_{0})^{2}}}$ | D. | R=R0$\root{3}{\frac{{t}_{0}}{{t}_{0}-{T}_{0}}}$ |
分析 先根据多转动一圈时间为t0,求出卫星的周期;然后再根据开普勒第三定律解得轨道半径.
解答 解:A行星发生最大偏离时,A、B行星与恒星在同一直线上且位于恒星同一侧,设行星B的运行周期为T、半径为R,则有:
$\frac{2π}{{T}_{0}}$t0-$\frac{2π}{T}$t0=2π,
所以T=$\frac{{{t}_{0}T}_{0}}{{{t}_{0}-T}_{0}}$,由开普勒第三定律得:$\frac{{R}_{0}^{3}}{{T}_{0}^{2}}$=$\frac{{R}^{3}}{{T}^{2}}$,
解得:R=R0$\root{3}{\frac{{{t}_{0}}^{2}}{({t}_{0}-{T}_{0})^{2}}}$,
故选:A.
点评 从本题可以看出,通过测量环绕天体的轨道半径和公转周期,可以求出中心天体的质量.

练习册系列答案
相关题目
6.下列说法中正确的是( )
| A. | 物体在恒力作用下,一定做直线运动 | |
| B. | 物体在始终与速度垂直且大小不变的力作用下,一定做匀速圆周运动 | |
| C. | 物体在变力作用下不可能做匀速圆周运动 | |
| D. | 物体在恒力作用下,不可能做圆周运动 |
16. 如图所示为一定质量的气体在P-V图中的A、B两个状态,已知气体在A状态的温度为127℃,则气体在B状态的温度约为( )
如图所示为一定质量的气体在P-V图中的A、B两个状态,已知气体在A状态的温度为127℃,则气体在B状态的温度约为( )
 如图所示为一定质量的气体在P-V图中的A、B两个状态,已知气体在A状态的温度为127℃,则气体在B状态的温度约为( )
如图所示为一定质量的气体在P-V图中的A、B两个状态,已知气体在A状态的温度为127℃,则气体在B状态的温度约为( )| A. | 63.5℃ | B. | 254℃ | C. | -73℃ | D. | 527℃ |
3.宇宙中存在着这样一种四星系统,这四颗星的质量相等,远离其他恒星,因此可以忽略其他恒星对它们的作用,四颗星稳定地分布在一个正方形的四个顶点上,且均围绕正方形对角线的交点做匀速圆周运动,假设每颗星的质量为m,正方形的边长为L,每颗星的半径为R,引力常量为G,则( )
| A. | 每颗星做圆周运动的半径为$\frac{1}{2}$L | |
| B. | 每颗星做圆周运动的向心力为$\frac{{({1+\sqrt{2}})G{m^2}}}{{2{L^2}}}$ | |
| C. | 每颗星表面的重力加速度为$\frac{Gm}{R^2}$ | |
| D. | 每颗星做圆周运动的周期为$2π\sqrt{\frac{{\sqrt{2}{L^3}}}{{(1+2\sqrt{2})Gm}}}$ |
13.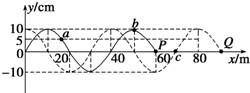 一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
 一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )| A. | 这列波的波速可能为50m/s | |
| B. | 从t+0.6 s时刻开始,经过0.5T,质点b沿x轴正方向运动20m | |
| C. | 质点c在这段时间内通过的路程可能为60 cm | |
| D. | 若T=0.8s,则当t+0.5s时刻,质点b、P的位移相同 | |
| E. | 若T=0.8s,当t+0.4s时刻开始计时,则质点c的振动方程为y=0.1sin($\frac{5}{2}$πt)(m) |
20.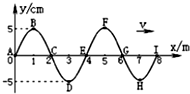 如图所示是一列简谐波在t=0时的波形图象,波速为v=l0m/s,此时波恰好传到I点,下列说法中正确的是( )
如图所示是一列简谐波在t=0时的波形图象,波速为v=l0m/s,此时波恰好传到I点,下列说法中正确的是( )
 如图所示是一列简谐波在t=0时的波形图象,波速为v=l0m/s,此时波恰好传到I点,下列说法中正确的是( )
如图所示是一列简谐波在t=0时的波形图象,波速为v=l0m/s,此时波恰好传到I点,下列说法中正确的是( )| A. | 此列波的周期为T=0.4s | |
| B. | 质点B、F在振动过程中位移总是相等 | |
| C. | 质点I的起振方向沿y轴负方向 | |
| D. | 当t=5.1s时,x=l0m的质点处于平衡位置处向下运动 | |
| E. | 质点A、C、E、G、I在振动过程中位移总是相同 |
18. 将一带有半球形凹槽的滑块放置在粗糙的水平面上,一表面光滑的小球置于凹槽的最低点,现对小球施加一水平向右的力F,使小球沿球面缓慢地上升,整个过程中滑块始终处于静止状态,假设地面所受的压力为F1.凹槽对小球的支持力为F2,地面对滑块的摩擦力为F3,则下列说法正确的是( )
将一带有半球形凹槽的滑块放置在粗糙的水平面上,一表面光滑的小球置于凹槽的最低点,现对小球施加一水平向右的力F,使小球沿球面缓慢地上升,整个过程中滑块始终处于静止状态,假设地面所受的压力为F1.凹槽对小球的支持力为F2,地面对滑块的摩擦力为F3,则下列说法正确的是( )
 将一带有半球形凹槽的滑块放置在粗糙的水平面上,一表面光滑的小球置于凹槽的最低点,现对小球施加一水平向右的力F,使小球沿球面缓慢地上升,整个过程中滑块始终处于静止状态,假设地面所受的压力为F1.凹槽对小球的支持力为F2,地面对滑块的摩擦力为F3,则下列说法正确的是( )
将一带有半球形凹槽的滑块放置在粗糙的水平面上,一表面光滑的小球置于凹槽的最低点,现对小球施加一水平向右的力F,使小球沿球面缓慢地上升,整个过程中滑块始终处于静止状态,假设地面所受的压力为F1.凹槽对小球的支持力为F2,地面对滑块的摩擦力为F3,则下列说法正确的是( )| A. | F1增大、F2增大、F3增大、F增大 | B. | F1不变,F2增大、F3增大、F增大 | ||
| C. | F1不变、F2增大、F3不变、F不变 | D. | F1减少、F2增大、F3增大、F不变 |
