题目内容
17.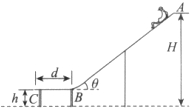 水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:(1)运动员从B滑到C的过程中克服摩擦力所做的功;
(2)运动员从A滑到B的过程中克服摩擦力所做的功;
(3)运动员到达C点时的速度大小.
分析 (1)先求得摩擦力,然后根据功的定义式求解;
(2)同(1)相似,先求得摩擦力,然后根据功的定义式求解;
(3)对运动员从A到C的运动过程应用动能定理即可求解.
解答 解:(1)运动员在BC轨道上,所受摩擦力fBC=μmg=90N,那么运动员从B滑到C的过程中克服摩擦力所做的功W=fBCd=180J;
(2)运动员在AB轨道上,所受摩擦力fAB=μmgcos37°=72N,那么运动员从A滑到B的过程中克服摩擦力所做的功$W′={f}_{AB}\frac{H-h}{sinθ}=720J$;
(3)运动员从A到C只有重力、摩擦力做功,故由动能定理可得:$mg(H-h)-W-W′=\frac{1}{2}m{{v}_{C}}^{2}-0$,所以,${v}_{C}=\sqrt{\frac{2[mg(H-h)-W-W′]}{m}}$=$3\sqrt{10}m/s$;
答:(1)运动员从B滑到C的过程中克服摩擦力所做的功为180J;
(2)运动员从A滑到B的过程中克服摩擦力所做的功为720J;
(3)运动员到达C点时的速度大小为$3\sqrt{10}m/s$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
相关题目
5. 两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )
两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )
 两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )
两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )| A. | a、b两点的场强相同 | |
| B. | 电荷从a点移到b点静电力不做功 | |
| C. | a、b、c三点的电势都大于无穷远处的电势 | |
| D. | 两个等量异种电荷的连线上c点场强最强 |
12. 现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
 现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压U恒定,某粒子在入口处从静止开始被加速电场加速,经匀强磁场B偏转后从出口离开磁场.若已知B和U,则( )| A. | 可以确定该粒子一定带负电 | B. | 可以测得该粒子的带电量 | ||
| C. | 不能测得该粒子的比荷 | D. | 可以测得该粒子的离开磁场的速度 |
6. 如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )
如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )
 如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )
如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )| A. | 2m/s | B. | 2$\sqrt{3}$m/s | C. | 4m/s | D. | 3m/s |
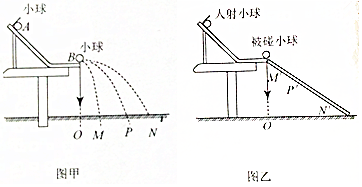
 如图所示,左侧的光滑斜面与右侧木板相连,把质量为m=l kg的滑块从斜面上高度h=0.1m处由静止释放,当右侧木板水平放置时,滑块在水平木板上滑行l=0.2m停止.欲使滑块从左侧斜面同一高度由静止下滑,并将右侧的木板向上转动一个锐角θ,形成斜面,使滑块在右侧木板上最远滑行0.l m,假设滑块由左侧斜面底端滑上右侧木板的瞬间速度大小不变.重力加速度g=10m/s2.求:θ的大小及滑块从冲上右侧木板到第一次返回最低点所用的时间.
如图所示,左侧的光滑斜面与右侧木板相连,把质量为m=l kg的滑块从斜面上高度h=0.1m处由静止释放,当右侧木板水平放置时,滑块在水平木板上滑行l=0.2m停止.欲使滑块从左侧斜面同一高度由静止下滑,并将右侧的木板向上转动一个锐角θ,形成斜面,使滑块在右侧木板上最远滑行0.l m,假设滑块由左侧斜面底端滑上右侧木板的瞬间速度大小不变.重力加速度g=10m/s2.求:θ的大小及滑块从冲上右侧木板到第一次返回最低点所用的时间. 如图所示,竖直平面内有一段粗糙的斜直轨道与光滑的圆形轨道相切,切点P与圆心O的连线与竖直方向的夹角为θ=53°,圆形轨道的半径为R,圆轨道的最低点B固定在水平地面上,一质量为m的小物块从斜轨道上A点由静止开始下滑,然后沿圆形轨道运动,物块刚好能通过圆形轨道最高点C,已知物块与斜轨道间的动摩擦因数μ=0.5,sin53°=0.8,cos53°=0.6,重力加速度为g=10m/s2,求:
如图所示,竖直平面内有一段粗糙的斜直轨道与光滑的圆形轨道相切,切点P与圆心O的连线与竖直方向的夹角为θ=53°,圆形轨道的半径为R,圆轨道的最低点B固定在水平地面上,一质量为m的小物块从斜轨道上A点由静止开始下滑,然后沿圆形轨道运动,物块刚好能通过圆形轨道最高点C,已知物块与斜轨道间的动摩擦因数μ=0.5,sin53°=0.8,cos53°=0.6,重力加速度为g=10m/s2,求: 如图所示,在光滑水平面AB与竖直平面内的半圆形导轨(轨道半径为R)在B点平滑连接,质量为m的小物块静止在A处,小物块立即获得一个向右的初速度,当它经过半圆形轨道的最低点B点时,对导轨的压力为其重力的9倍,之后沿轨道运动恰能通过半圆形轨道的最高点C点,重力加速度为g,求:
如图所示,在光滑水平面AB与竖直平面内的半圆形导轨(轨道半径为R)在B点平滑连接,质量为m的小物块静止在A处,小物块立即获得一个向右的初速度,当它经过半圆形轨道的最低点B点时,对导轨的压力为其重力的9倍,之后沿轨道运动恰能通过半圆形轨道的最高点C点,重力加速度为g,求: 如图所示,在离水面高H的岸边有人以大小为V0的速度匀速收绳使船靠岸.当船与岸上的定滑轮水平距离为S时,船速是多大?
如图所示,在离水面高H的岸边有人以大小为V0的速度匀速收绳使船靠岸.当船与岸上的定滑轮水平距离为S时,船速是多大?