题目内容
9. 如图所示,在光滑水平面AB与竖直平面内的半圆形导轨(轨道半径为R)在B点平滑连接,质量为m的小物块静止在A处,小物块立即获得一个向右的初速度,当它经过半圆形轨道的最低点B点时,对导轨的压力为其重力的9倍,之后沿轨道运动恰能通过半圆形轨道的最高点C点,重力加速度为g,求:
如图所示,在光滑水平面AB与竖直平面内的半圆形导轨(轨道半径为R)在B点平滑连接,质量为m的小物块静止在A处,小物块立即获得一个向右的初速度,当它经过半圆形轨道的最低点B点时,对导轨的压力为其重力的9倍,之后沿轨道运动恰能通过半圆形轨道的最高点C点,重力加速度为g,求:(1)小物块的初动能.
(2)小物块从B点到C点克服摩擦力做的功.
分析 (1)由牛顿第二定律求得物块在B点的速度,然后根据物块从A到B做匀速直线运动,故动能不变来求解;
(2)根据牛顿第二定律求得物块在C点的速度,然后对B到C的运动过程应用动能定理即可求解.
解答 解:(1)小物块经过半圆形轨道的最低点B点时,对导轨的压力为其重力的9倍,故由牛顿第二定律可得:$9mg-mg=\frac{m{{v}_{B}}^{2}}{R}$;
又有小物块在AB上运动,合外力为零,物块做匀速直线运动,故动能不变,所以,小物块的初动能${E}_{k0}=\frac{1}{2}m{{v}_{B}}^{2}=4mgR$;
(2)小物块恰能通过半圆形轨道的最高点C点,故对小物块在C点应用牛顿第二定律可得:$mg=\frac{m{{v}_{C}}^{2}}{R}$;
物块从B到C的运动过程,只有重力、摩擦力做功,故由动能定理可得:$-2mgR+{W}_{f}=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}mgR-4mgR=-\frac{7}{2}mgR$;
所以,${W}_{f}=-\frac{3}{2}mgR$,故小物块从B点到C点克服摩擦力做的功为$\frac{3}{2}mgR$;
答:(1)小物块的初动能为4mgR.
(2)小物块从B点到C点克服摩擦力做的功为$\frac{3}{2}mgR$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
相关题目
9.已知入射角i=60°,b光在三棱镜中的折射角r=45°,该三棱镜对b光的折射率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
14.目前,在居室装修中经常用到花岗岩、大理石等装饰材料,这些岩石都不同程度含有放射性元素,比如,有些含有铀、钍的花岗岩等岩石会释放出放射性情性气体氡,而氡会发生放射性衰变,放射出α、β、γ射线,这些射线会导致细胞发生癌变及呼吸道等方面的疾病,根据有关放射性知识可知,下列说法正确的是( )
| A. | 已知氡的半衰期为3.8天,若取4个氡原子核,经7.6天后就一定剩下一个氡原子核 | |
| B. | 把放射性元素放在密封的容器中,可以减慢放射性元素衰变的速度 | |
| C. | 降低温度或增大压强,让该元素与其他物质形成化合物,均可以减小衰变速度 | |
| D. | 放射性元素的半衰期越短,表明有半数原子核发生衰变所需要的时间越短,衰变越快 |
1. 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )| A. | b的伸长量为L | B. | b的伸长量为$\frac{{k}_{2}L}{{k}_{1}}$ | ||
| C. | 小球质量为$\frac{{k}_{1}L}{g}$ | D. | 小球质量为$\frac{{k}_{2}L}{g}$ |





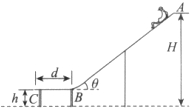 水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
 如图,将质量为m的小钢珠以某一初速度v0从A点无撞击地进入两$\frac{1}{4}$圆管组成的竖直细管道,经最高点B水平射出后落到斜面上C点,两圆心O、O′连线水平,O′为斜面的顶点,已知斜面与竖直线BO′夹角θ=60°,两圆管的半径均为R,O′C=R,重力加速度g,求
如图,将质量为m的小钢珠以某一初速度v0从A点无撞击地进入两$\frac{1}{4}$圆管组成的竖直细管道,经最高点B水平射出后落到斜面上C点,两圆心O、O′连线水平,O′为斜面的顶点,已知斜面与竖直线BO′夹角θ=60°,两圆管的半径均为R,O′C=R,重力加速度g,求
