题目内容
6. 如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )
如图所示,一小船位于100m宽的河的正中央A点处,从这里向下游50$\sqrt{3}$m处有一危险区,当时水流速度为6m/s,为了使小船避开危险区直线到达对岸,那么小船航行的最小速度(静水中)为( )| A. | 2m/s | B. | 2$\sqrt{3}$m/s | C. | 4m/s | D. | 3m/s |
分析 小船离河岸50m处,要使能安全到达河岸,求出小船运动最大位移.最大位移的方向即为合速度方向,因此由水流速度与小船的合速度,借助于平行四边形定则,即可求出小船在静水中最小速度.
解答 解:要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为x=$\sqrt{5{0}^{2}+(50\sqrt{3})^{2}}$m=100m,
因此已知小船能安全到达河岸的合速度,设此速度与水流速度的夹角为θ,
即有tanθ=$\frac{50}{50\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,所以θ=30°,
又已知流水速度,则可得小船在静水中最小速度为:v船=v水 sinθ=$\frac{1}{2}$×6m/s=3m/s,故ABC错误、D正确;
故选:D.
点评 本题属于:一个速度要分解,已知一个分速度的大小与方向,还已知另一个分速度的大小且最小,则求这个分速度的方向与大小值.这种题型运用平行四边形定则,由几何关系来确定最小值.

练习册系列答案
相关题目
14.目前,在居室装修中经常用到花岗岩、大理石等装饰材料,这些岩石都不同程度含有放射性元素,比如,有些含有铀、钍的花岗岩等岩石会释放出放射性情性气体氡,而氡会发生放射性衰变,放射出α、β、γ射线,这些射线会导致细胞发生癌变及呼吸道等方面的疾病,根据有关放射性知识可知,下列说法正确的是( )
| A. | 已知氡的半衰期为3.8天,若取4个氡原子核,经7.6天后就一定剩下一个氡原子核 | |
| B. | 把放射性元素放在密封的容器中,可以减慢放射性元素衰变的速度 | |
| C. | 降低温度或增大压强,让该元素与其他物质形成化合物,均可以减小衰变速度 | |
| D. | 放射性元素的半衰期越短,表明有半数原子核发生衰变所需要的时间越短,衰变越快 |
1. 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
 如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )
如图所示,轻质弹簧a、b劲度系数分别为k1和k2,两弹簧串接在一起,a上端固定,b下端栓接一小球,稳定后a的伸长量为L.已知重力加速度为g,则( )| A. | b的伸长量为L | B. | b的伸长量为$\frac{{k}_{2}L}{{k}_{1}}$ | ||
| C. | 小球质量为$\frac{{k}_{1}L}{g}$ | D. | 小球质量为$\frac{{k}_{2}L}{g}$ |
11.下列各图中物体m满足机械能守恒的是(均不计空气阻力)( )

| A. | 甲图小球m绕O点来回摆动 | |
| B. | 乙图物块m沿固定斜面匀速下滑 | |
| C. | 丙图物块m在力F作用下沿光滑固定斜面上滑 | |
| D. | 丁图小球m沿粗糙半圆形固定轨道下滑 |
15. 如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )
如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )
 如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )
如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )| A. | 球被击出后做平抛运动 | |
| B. | 球被击出时的初速度大小为L$\sqrt{\frac{g}{2h}}$ | |
| C. | 该球被击出到落入A穴所用时间为$\sqrt{\frac{h}{2g}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgL}{h}$ |
16.下面哪些应用是利用了多普勒效应( )
| A. | 雨天、雾天的时候红灯更容易被发现 | |
| B. | 有经验的战士从炮弹飞行的尖叫声判断飞行炮弹是接近还是远去 | |
| C. | 铁路工人用耳贴在铁轨上可判断火车的运行情况 | |
| D. | 过去的剑客睡觉时用剑鞘做枕头 |
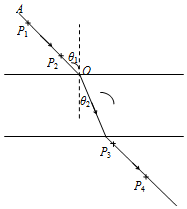 某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.
某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行.正确操作后,作出的光路图及测出的相关角度如图所示.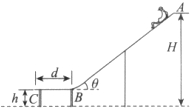 水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求:
水上滑梯可简化成如图所示的模型,倾角为θ=37°斜滑道AB和水平滑道BC平滑连接.起点A距水面的高度H=8.0m,BC长d=2.0m,端点C距水面的高度h=2.0m,一质量m=60kg的运动员从滑道起点A点无初速地自由滑下,不计空气阻力(取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点).已知运动员与AB、BC间有摩擦力,且动摩擦因数均为μ=0.15,求: 如图,将质量为m的小钢珠以某一初速度v0从A点无撞击地进入两$\frac{1}{4}$圆管组成的竖直细管道,经最高点B水平射出后落到斜面上C点,两圆心O、O′连线水平,O′为斜面的顶点,已知斜面与竖直线BO′夹角θ=60°,两圆管的半径均为R,O′C=R,重力加速度g,求
如图,将质量为m的小钢珠以某一初速度v0从A点无撞击地进入两$\frac{1}{4}$圆管组成的竖直细管道,经最高点B水平射出后落到斜面上C点,两圆心O、O′连线水平,O′为斜面的顶点,已知斜面与竖直线BO′夹角θ=60°,两圆管的半径均为R,O′C=R,重力加速度g,求