题目内容
17. 如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )
如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )| A. | 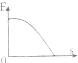 | B. |  | C. | 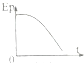 | D. | 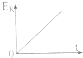 |
分析 根据动能定理、重力势能表达式EP=mgh,得到动能Ek与重力势能Ep与x的关系式.物体克服摩擦力做功等于其机械能的减少,得到机械能E机与x的表达式;克服摩擦力做功由功的计算公式得到.根据这些表达式再选择图象
解答 解:设斜面的倾角为θ.物体所受的滑动摩擦力大小为f,由牛顿第二定律可知mgsinθ-f=ma,物体做匀加速运动.
A、根据功能关系得:取斜面低端为零势能面,开始时滑块机械能为:E机=mgssinθ,滑块下滑过程中机械能的变化量等于除重力外其余力做的功,机械能的变化为△E=Wf,由于滑块下滑过程中,受到摩擦力作用,且做负功,机械能E=mgssinθ-fs.E与s成正比且随着s的增大而减小,则E-s是倾斜不过原点的直线,故A错误.
B、根据动能定理得:Ek=(mgsinθ-f)s,可知,Ek∝s,则Ek-s是过原点的倾斜的直线,故B错误.
C、取斜面底端为零势能面,最高点到最低端的距离为H,物体做匀加速运动,s=$\frac{1}{2}a{t}^{2}$,重力势能:EP=mgh=mgH-mgssinθ=mgH-mg$\frac{1}{2}a{t}^{2}$sinθ,随时间增加,重力势能与t是二次函数关系,故C正确;
D、物体下滑过程中做匀加速运动,故:${E}_{k}=\frac{1}{2}m{v}^{2}=\frac{1}{2}m{a}^{2}{t}^{2}$,故动能与时间是二次函数关系,故D错误;
故选:C
点评 解决本题的关键要掌握功的公式W=Fscosθ,以及会灵活运用动能定理和功能关系,根据解析式再分析图象

练习册系列答案
相关题目
12. 真空中一点电荷形成的电场中的部分电场线如图所示,分别标记为1、2、3、4、5,且1、5和2、4分别关于3对称.以电场线上3上的某点为圆心画一个圆,圆与各电场线的交点分别为a、b、c、d、e,则下列说法中正确的是( )
真空中一点电荷形成的电场中的部分电场线如图所示,分别标记为1、2、3、4、5,且1、5和2、4分别关于3对称.以电场线上3上的某点为圆心画一个圆,圆与各电场线的交点分别为a、b、c、d、e,则下列说法中正确的是( )
 真空中一点电荷形成的电场中的部分电场线如图所示,分别标记为1、2、3、4、5,且1、5和2、4分别关于3对称.以电场线上3上的某点为圆心画一个圆,圆与各电场线的交点分别为a、b、c、d、e,则下列说法中正确的是( )
真空中一点电荷形成的电场中的部分电场线如图所示,分别标记为1、2、3、4、5,且1、5和2、4分别关于3对称.以电场线上3上的某点为圆心画一个圆,圆与各电场线的交点分别为a、b、c、d、e,则下列说法中正确的是( )| A. | 电场强度Ea<Ec | |
| B. | 电势φb=φd | |
| C. | 将一正电荷由a点移到d点,电场力做负功 | |
| D. | 将一负电荷由b点移到e点,电势能减小 |
2.有关分子动理论和物体的内能,下列叙述正确的是( )
| A. | 物体吸热,内能一定增加 | |
| B. | 布朗运动指的是分子的热运动 | |
| C. | 气体的压强是由于大量分子频繁撞击器壁产生的 | |
| D. | 根据油膜实验可知分子在永不停息地做无规则运动 |
7.关于物理学中的一些研究方法,下列说法正确的是( )
| A. | 探究力的平行四边形定则的实验中采用了理想模型法 | |
| B. | 卡文迪许测定引力常量G的数值时采用了微小量放大的方法 | |
| C. | 伽利略在利用理想实验探究力和运动关系时采用了等效替代法 | |
| D. | 法拉第利用电场线描绘电场是采用了归纳法 |

 如图所示,在磁感应强度B为的0.4T的匀强磁场中,让长0.2m的导体ab在金属框上以6m/s的速度向右移动.此时感应电动势的大小是多少?如果R1=6Ω,R2=3Ω,其余部分电阻不计.则通过ab的电流是多少?
如图所示,在磁感应强度B为的0.4T的匀强磁场中,让长0.2m的导体ab在金属框上以6m/s的速度向右移动.此时感应电动势的大小是多少?如果R1=6Ω,R2=3Ω,其余部分电阻不计.则通过ab的电流是多少? 如图,两平行金属板A、B长l=8cm,两板间距离d=8cm,B板比A板电势高300V,即UBA=300V.一带正电的粒子电量q=1×10-10C,质量m=1×10-20kg,以初速度v0=2×106m/s,从R点沿电场中心线RO垂直电场方向射入电场,粒子飞出电场后经过无场区域,进入界面MN、PQ间匀强磁场区域,从磁场的PQ边界出来后刚好打在中心线上的S点,已知MN边界与平行板的右端相距为L,两界面MN、PQ相距为L,S点到PQ边界的距离为$\frac{4}{3}$L,且L=12cm,粒子重力及空气阻力忽略不计.求:
如图,两平行金属板A、B长l=8cm,两板间距离d=8cm,B板比A板电势高300V,即UBA=300V.一带正电的粒子电量q=1×10-10C,质量m=1×10-20kg,以初速度v0=2×106m/s,从R点沿电场中心线RO垂直电场方向射入电场,粒子飞出电场后经过无场区域,进入界面MN、PQ间匀强磁场区域,从磁场的PQ边界出来后刚好打在中心线上的S点,已知MN边界与平行板的右端相距为L,两界面MN、PQ相距为L,S点到PQ边界的距离为$\frac{4}{3}$L,且L=12cm,粒子重力及空气阻力忽略不计.求:
 如图为氢原子能级的示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时,可辐射6种不同频率的光子;其中有3种频率的光子能使逸出功为6.34eV的金属铂发生光电效应.
如图为氢原子能级的示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时,可辐射6种不同频率的光子;其中有3种频率的光子能使逸出功为6.34eV的金属铂发生光电效应.