题目内容
9.如图所示,两个斜面AB和CD的倾角分别为α和β,且均与水平面BC平滑连接.水平面的C端静止地放置一质量为m的物块,在斜面AB上一质量为M的物块加速下滑,冲至水平面后与物块m碰撞前瞬间速度为v0,碰撞后合为一体冲上斜面CD,物块与斜面的动摩擦因数均为μ,重力加速度为g.求:
(1)物体M在斜面AB上运动时的加速度a;
(2)两物体碰后的共同速度v;
(3)能冲上斜面CD的最大高度H.
分析 (1)根据受力分析由牛顿第二定律求得物体在斜面AB上运动时的加速度;
(2)根据水平方向动量守恒求得碰撞后两者的共同速度v;
(3)根据动能定理求得物块在斜面上上升的最大距离从而求得上升的最大高度H.
解答 解:(1)在AB斜面上对物体进行受力分析,根据牛顿第二定律有:
垂直斜面方向有:N-Mgcosα=0 ①
沿斜面向下有:Mgsinα-f=Ma ②
又f=μN ③
由①②③可解得加速度a=gsinα-μgcosα
(2)两物体碰撞过程中水平方向满足动量守恒,故有:
Mv0=(M+m)v
可得碰撞后整体的速度v=$\frac{M}{M+m}$v0
(3)碰撞后物体在斜面CD上运动时只有重力和阻力做功,根据动能定理有:
$-μ(M+m)gcosβ•\frac{H}{sinβ}-(M+m)gH$=0-$\frac{1}{2}$(M+m)v2
可解得:H=$\frac{{{M^2}V_0^2sinβ}}{{2{{(M+m)}^2}g(sinβ+μcosβ)}}$
答:(1)物体M在斜面AB上运动时的加速度a为gsinα-μgcosα;
(2)两物体碰后的共同速度v为$\frac{M}{M+m}$;
(3)能冲上斜面CD的最大高度H为$\frac{{{M^2}V_0^2sinβ}}{{2{{(M+m)}^2}g(sinβ+μcosβ)}}$.
点评 本题考查了牛顿第二定律和动能定理的基本运用,掌握规律是正确解题的关键,对于第3问也可以采用动力学知识求解,但是没有运用动能定理解答方便.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.若某恒星系中所有天体的密度增大为原来的2倍,天体的直径和天体间的距离不变,某行星绕该恒星做匀速圆周运动,则下列关于运行参量变化的描述正确的是( )
| A. | 行星绕该恒星做匀速圆周运动的向心力变为原来的2倍 | |
| B. | 行星绕该恒星做匀速圆周运动的线速度变为原来的2倍 | |
| C. | 行星绕该恒星做匀速圆周运动的角速度变为原来的2倍 | |
| D. | 行星绕该恒星做匀速圆周运动的周期变为原来的$\frac{\sqrt{2}}{2}$倍 |
17.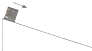 如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )
如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )
 如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )
如图所示,滑块由静止开始沿表面粗糙的固定斜面下滑,对于该运动过程,若用E、EP、Ek、s、t分别表示滑块的机械能、重力势能、动能、位移和时间,则下列图象中能正确描述这一运动规律的是( )| A. | 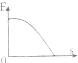 | B. |  | C. | 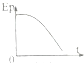 | D. | 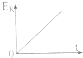 |
14.甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,下列说法正确的是( )
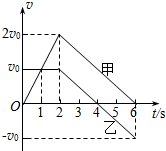

| A. | t=1s时甲和乙相遇 | |
| B. | t=2s时甲的速度方向反向 | |
| C. | t=4s时乙的加速度方向反向 | |
| D. | 0~2s内甲的位移与0~6s内乙的位移相等 |
19.根据《中国广播电视报》报道,在暑天就诊的小病人,低锌发病率高达60%以上.由于锌对人体代谢起着重要作用,因此儿童生长发育时期测量体内含锌量已成为体格检查的重要内容之一,也引起了我国科技工作者的高度重视.其中比较简单的一种检测方法是取儿童的头发约50g,放在核反应堆中经中子轰击后,头发中的锌元素与中子反应生成具有放射性的同位素锌,其核反应方程式为${\;}_{30}^{64}$Zn+${\;}_{0}^{1}$n→${\;}_{30}^{65}$Zn.${\;}_{30}^{65}$Zn衰变放射出能量为1115eV的γ射线,通过测定γ射线的强度可以计算出头发中锌的含量.关于以上叙述,下列说法正确的是 ( )
| A. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn有相同的核子数 | |
| B. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn具有相同的质子数 | |
| C. | γ射线是由锌原子的内层电子受到激发而产生的 | |
| D. | γ射线在真空中传播的速度是3.0×108m/s |
 如图所示,在水平地面上固定一倾角为θ的斜面体,斜面的顶端高为h处有甲、乙两物体(均可视为质点).现将物体甲以某一速度大小水平抛出,同时让物体乙以相同的速度大小开始沿光滑斜面滑下,结果两物体能同时到达水平地面.忽略空气阻力,求甲、乙两物体刚落到水平地面时的距离L.
如图所示,在水平地面上固定一倾角为θ的斜面体,斜面的顶端高为h处有甲、乙两物体(均可视为质点).现将物体甲以某一速度大小水平抛出,同时让物体乙以相同的速度大小开始沿光滑斜面滑下,结果两物体能同时到达水平地面.忽略空气阻力,求甲、乙两物体刚落到水平地面时的距离L. 某列简谐横波在t=0时刻的波形如图所示,若该横波沿x轴正方向传播,且波速v=4m/s,则x=8m处的质点的振动图象是下列图象中的( )
某列简谐横波在t=0时刻的波形如图所示,若该横波沿x轴正方向传播,且波速v=4m/s,则x=8m处的质点的振动图象是下列图象中的( )



 如图所示,某透明介质的截面为直角三角形ABC,其中∠A=30°,AC边长为L,一束单色光从AC面上距A为$\frac{L}{3}$的D点垂直于AC面射入,恰好在AB面发生全反射,已知该光束从射入该介质经最短时间t又到达AC面,设真空中的光速为c,求:
如图所示,某透明介质的截面为直角三角形ABC,其中∠A=30°,AC边长为L,一束单色光从AC面上距A为$\frac{L}{3}$的D点垂直于AC面射入,恰好在AB面发生全反射,已知该光束从射入该介质经最短时间t又到达AC面,设真空中的光速为c,求: 如图所示,倾角为30°的光滑斜面固定在水平地面上.劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量为m的物体A(可视为质点)连接.细绳的一端系在物体A上,细绳有小挂钩的另一端跨过不计摩擦的定滑轮(小挂钩和细绳的质量不计),细绳与斜面平行.小挂钩不挂任何物体时,物体A静止于P点;在小挂钩上轻轻挂上一个质量也为m的物块B后,物体A沿斜面向上运动,物体A经过Q点位置时速度最大.斜面足够长,运动过程中物块B始终未接触地面,重力加速度大小为g,求:
如图所示,倾角为30°的光滑斜面固定在水平地面上.劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量为m的物体A(可视为质点)连接.细绳的一端系在物体A上,细绳有小挂钩的另一端跨过不计摩擦的定滑轮(小挂钩和细绳的质量不计),细绳与斜面平行.小挂钩不挂任何物体时,物体A静止于P点;在小挂钩上轻轻挂上一个质量也为m的物块B后,物体A沿斜面向上运动,物体A经过Q点位置时速度最大.斜面足够长,运动过程中物块B始终未接触地面,重力加速度大小为g,求: