题目内容
19.质量为1kg的物体沿倾角为37°、长为3m的光滑斜面,从斜面顶端由静止下滑到斜面底端,该过程中物体重力的平均功率为18W,到达斜面底端时物体的重力的瞬时功率为36W (取g=10m/s2)分析 根据牛顿第二定律求出物体下滑的加速度,根据位移时间公式求出运动的时间,结合重力做功的大小,运用平均功率的公式求出重力的平均功率.根据速度时间公式求出物体到达底端的速度,结合瞬时功率的公式求出重力的瞬时功率大小.
解答 解:根据牛顿第二定律得,物体的加速度为:
a=$\frac{mgsin37°}{m}=gsin37°=10×0.6m/{s}^{2}$=6m/s2,
根据x=$\frac{1}{2}a{t}^{2}$得:t=$\sqrt{\frac{2x}{a}}=\sqrt{\frac{2×3}{6}}s=1s$,
则重力做功的平均功率为:$\overline{P}=\frac{mgxsin37°}{t}=\frac{10×3×0.6}{1}W=18W$.
物体到达底端的速度为:v=at=6×1m/s=6m/s,
重力的瞬时功率为:P=mgvsin37°=10×6×0.6W=36W.
故答案为:18,36.
点评 解决本题的关键知道瞬时功率和平均功率的区别,掌握这两种功率的求法,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
 如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )| A. | A球经过面1时的速率等于B球经过面1时的速率 | |
| B. | A球从面1到面2的速率变化等于B球从面1到面2的速率变化 | |
| C. | A球从面1到面2的动量变化大于B球从面1到面2的动量变化 | |
| D. | A球从面1到面2的机械能变化等于B球从面1到面2的机械能变化 |
14. 如图所示,一导线弯成边长为L的正三角形闭合回路.虚线MN右侧有磁感应强度为B的匀强进场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直线CD边始终与MN垂直.从C点到达边界开始到D点进入磁场的过程中,下列结论正确的是( )
如图所示,一导线弯成边长为L的正三角形闭合回路.虚线MN右侧有磁感应强度为B的匀强进场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直线CD边始终与MN垂直.从C点到达边界开始到D点进入磁场的过程中,下列结论正确的是( )
 如图所示,一导线弯成边长为L的正三角形闭合回路.虚线MN右侧有磁感应强度为B的匀强进场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直线CD边始终与MN垂直.从C点到达边界开始到D点进入磁场的过程中,下列结论正确的是( )
如图所示,一导线弯成边长为L的正三角形闭合回路.虚线MN右侧有磁感应强度为B的匀强进场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直线CD边始终与MN垂直.从C点到达边界开始到D点进入磁场的过程中,下列结论正确的是( )| A. | 感应电流方向改变 | B. | CD段直线始终不受安培力 | ||
| C. | 导线中的感应电流大小不变 | D. | 感应电动势最大值$\frac{\sqrt{3}BLv}{2}$ |
8.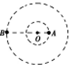 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )| A. | A星球的轨道半径为R=$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$L | |
| B. | B星球的轨道半径为r=$\frac{{m}_{2}}{{m}_{1}}$L | |
| C. | 双星运行的周期为T=2πL$\sqrt{\frac{L}{G({m}_{1}+{m}_{2})}}$ | |
| D. | 若近似认为B星球绕A星球中心做圆周运动,则B星球的运行周期为T=2πL$\sqrt{\frac{L}{G{m}_{1}}}$ |

 如图的电路中,电池组的电动势E=30伏,电阻R2=10欧,两个水平放置的带电金属板间的距离d=1.5厘米在金属板间的匀强电场中,有一质量为m=7×10-8千克带电量q=-7.0×10-10库仑的油滴,当把可变电阻器R3的阻值调到30欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试求:
如图的电路中,电池组的电动势E=30伏,电阻R2=10欧,两个水平放置的带电金属板间的距离d=1.5厘米在金属板间的匀强电场中,有一质量为m=7×10-8千克带电量q=-7.0×10-10库仑的油滴,当把可变电阻器R3的阻值调到30欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试求: 电饭煲的工作原理如图所示,可分为两部分,即控制部分:由S2、R1和黄灯组成,工作(加热)部分;有发热电阻R3、R2和红灯组成,S1是一个磁钢限温开关,手动闭合,当此开关的温度达到居里点(103℃)时,自动断开,且不能自动复位,S2是一个双金属片自动开关,当温度达到70℃-80℃时,自动断开,低于70℃时,自动闭合,红灯、黄灯是指示灯,通过其电流必须较小,所以R1、R2起限流作用,R3是发热电阻.接通电源并按下S1后,黄灯熄而红灯亮,R3发热,当温度达到70℃-80℃时,S2断开,当温度达到103℃时饭熟,S1断开,当温度降到70℃以下时,S2闭合,电饭煲处于保温状态,由以上描述可知R2>R3(填<或﹦或>),若用电饭煲烧水时,S1不会(填“会”或“不会”)自动断开.
电饭煲的工作原理如图所示,可分为两部分,即控制部分:由S2、R1和黄灯组成,工作(加热)部分;有发热电阻R3、R2和红灯组成,S1是一个磁钢限温开关,手动闭合,当此开关的温度达到居里点(103℃)时,自动断开,且不能自动复位,S2是一个双金属片自动开关,当温度达到70℃-80℃时,自动断开,低于70℃时,自动闭合,红灯、黄灯是指示灯,通过其电流必须较小,所以R1、R2起限流作用,R3是发热电阻.接通电源并按下S1后,黄灯熄而红灯亮,R3发热,当温度达到70℃-80℃时,S2断开,当温度达到103℃时饭熟,S1断开,当温度降到70℃以下时,S2闭合,电饭煲处于保温状态,由以上描述可知R2>R3(填<或﹦或>),若用电饭煲烧水时,S1不会(填“会”或“不会”)自动断开.
 如图所示,光滑水平轨道上放置长板A(上表面粗糙)和滑块C,滑块B置于A的左端,三者质量分别为mA=2kg、mB=1kg、mC=2kg.开始时C静止,A、B一起以v0=5m/s的速度匀速向右运动,A与C发生碰撞(时间极短)后C向右运动,经过一段时间,A、B再次达到共同速度一起向右运动,且恰好不再与C发生碰撞.求
如图所示,光滑水平轨道上放置长板A(上表面粗糙)和滑块C,滑块B置于A的左端,三者质量分别为mA=2kg、mB=1kg、mC=2kg.开始时C静止,A、B一起以v0=5m/s的速度匀速向右运动,A与C发生碰撞(时间极短)后C向右运动,经过一段时间,A、B再次达到共同速度一起向右运动,且恰好不再与C发生碰撞.求