题目内容
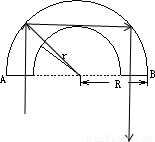
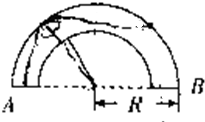
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=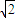 r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出.设透明柱体的折射率为n,光在透明柱体内传播的时间为t,若真空中的光速为c,则( )
r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出.设透明柱体的折射率为n,光在透明柱体内传播的时间为t,若真空中的光速为c,则( )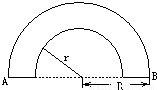
A.n可能为
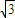
B.n可能为2
C.t可能为
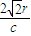
D.t可能为
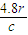
【答案】分析:由题意利用几何关系作出光路图可知第一次的入射角,即可判断临界角的大小,并能判断出折射率的大小范围;由光路图即可得出运行时间.
解答:解:只经过两次全反射可知第一次入射角为45°,反射光路图如图所示.根据全反射可知临界角C≤45°,再根据n=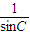 可知n≥
可知n≥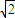 ,故AB均正确;
,故AB均正确;
光在透明柱体中运动路程为L=4r,运动时间为t=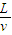 =
=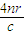 ,则t≥
,则t≥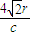 ,故CD均错.
,故CD均错.
故选AB.
点评:本题考查全反射,解题的关键在于题目中几何关系的应用,只有根据几何关系解出入射角才能求出正确结果.
解答:解:只经过两次全反射可知第一次入射角为45°,反射光路图如图所示.根据全反射可知临界角C≤45°,再根据n=
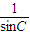 可知n≥
可知n≥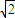 ,故AB均正确;
,故AB均正确;光在透明柱体中运动路程为L=4r,运动时间为t=
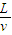 =
=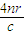 ,则t≥
,则t≥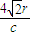 ,故CD均错.
,故CD均错.故选AB.

点评:本题考查全反射,解题的关键在于题目中几何关系的应用,只有根据几何关系解出入射角才能求出正确结果.

练习册系列答案
相关题目
 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 3 |
A、n可能为
| ||||
| B、n可能为2 | ||||
C、t可能为
| ||||
D、t可能为
|
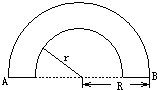 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 2 |
A、n可能为
| ||||
| B、n可能为1.2 | ||||
C、t可能为
| ||||
D、t可能为
|
 如图所示,空气中有一折射率为
如图所示,空气中有一折射率为 (2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
(2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=