题目内容
16. 一电场的电场强度E随时间t变化的图象如图所示,此电场中有一个带电粒子,在t=0时刻由静止释放,若带电粒子只受电场力作用,则下列判断正确的是( )
一电场的电场强度E随时间t变化的图象如图所示,此电场中有一个带电粒子,在t=0时刻由静止释放,若带电粒子只受电场力作用,则下列判断正确的是( )| A. | 带电粒子将向一个方向运动 | B. | 在l~3s内,电场力做功为零 | ||
| C. | 2s末带电粒子的速度为零 | D. | 在2~4s内,电场力做的功等于零 |
分析 从图中可以看出,电场变化的周期是3s,在每个周期的第一秒和三秒内,由电场力和牛顿第二定律可得出a2是a1的2倍,方向相反,从而分析带电粒子的运动情况;
1~3s的时间内,初速度不为零,末速度为零,做功不会为零;根据动量定理可计算出2~4s内的动量的变化,分析速度的变化,由动能定理判断2~4s内,电场力做的功情况.
解答 解:A、由图可知,带在第2s和第5s内的电场强度是第1s以及第3、4s内电场强度的2倍;由牛顿第二定律可知,带电粒子在每个周期的第一秒和三秒内,带电粒子的加速度大小为a1=$\frac{qU}{md}$,第二秒的加速度大小为a2=2$\frac{qU}{md}$,得a2=2a1,粒子在第1s内做初速度为零的匀加速运动,第2s内沿原方向做匀减速运动,1.5s末后开始反方向运动,2s末速度向左,故AC错误.
B、1~3s内,带电粒子的初速度不为零,末速度不为零,由动能定理可知电场力所做的功不为零,故B错误;
D、2~4s内,电场力的冲量为 I=2qE0×0.5+(-qE0)×1=0,由动量定理得知,初速度与末速度相等,由动能定理得知,电场力做功为零.故D正确.
故选:D.
点评 带电粒子在交变电场中运动的情况比较复杂,由于不同时段受力情况不同、运动情况也就不同,若按常规的分析方法,一般都较繁琐,所以较好的分析方法就是利用带电粒子的速度图象来分析.但需要掌握好图象的准确应用.

练习册系列答案
相关题目
7. 如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
 如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )| A. | $\frac{qR}{4BL}$ | B. | $\frac{qR}{2BL}$ | C. | $\frac{qR}{BL}$ | D. | $\frac{2qR}{BL}$ |
4. 如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为φC、φD,下列说法正确的是( )
如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为φC、φD,下列说法正确的是( )
 如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为φC、φD,下列说法正确的是( )
如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为φC、φD,下列说法正确的是( )| A. | EC与ED相同,φC与φD不相等 | B. | EC与ED不相同,φC与φD相等 | ||
| C. | EC与ED相同,φC与φD相等 | D. | EC与ED不相同,φC与φD不相等 |
11. 物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
 物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )| A. | μA>μB,mA<mB | B. | μA<μB,mA<mB | C. | μA>μB,mA>mB | D. | μA<μB,mA>mB |
1.某质点做直线运动,其速度随时间变化的v-t图象如图所示,则质点( )


| A. | 初速度大小是0 | B. | 初速度大小是lm/s | ||
| C. | 加速度大小是0.5m/s2 | D. | 加速度大小是1m/s2 |
5. 如图,三个等势面上有a、b、c、d四点,若将一正电荷由c经a移到d点,电场力做正功W1,若由c经b移到d点,电场力做正功W2,则W1与W2,c、d两点的电势φc,φd关系为( )
如图,三个等势面上有a、b、c、d四点,若将一正电荷由c经a移到d点,电场力做正功W1,若由c经b移到d点,电场力做正功W2,则W1与W2,c、d两点的电势φc,φd关系为( )
 如图,三个等势面上有a、b、c、d四点,若将一正电荷由c经a移到d点,电场力做正功W1,若由c经b移到d点,电场力做正功W2,则W1与W2,c、d两点的电势φc,φd关系为( )
如图,三个等势面上有a、b、c、d四点,若将一正电荷由c经a移到d点,电场力做正功W1,若由c经b移到d点,电场力做正功W2,则W1与W2,c、d两点的电势φc,φd关系为( )| A. | W1=W2 φc<φd | B. | W1=W2 φc>φd | C. | W1>W2 φc>φd | D. | W1<W2 φc<φd |
6. 如图所示为Ⅰ、Ⅱ、Ⅲ三个质点同时同地开始沿直线运动的位移一时间图象,则在时间t内( )
如图所示为Ⅰ、Ⅱ、Ⅲ三个质点同时同地开始沿直线运动的位移一时间图象,则在时间t内( )
 如图所示为Ⅰ、Ⅱ、Ⅲ三个质点同时同地开始沿直线运动的位移一时间图象,则在时间t内( )
如图所示为Ⅰ、Ⅱ、Ⅲ三个质点同时同地开始沿直线运动的位移一时间图象,则在时间t内( )| A. | 它们的位移相等 | B. | 它们的路程相等 | ||
| C. | Ⅰ的平均速度最大 | D. | 它们的平均速度相等 |
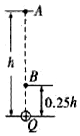 如图所示,Q为固定的正点电荷,A、B两点在Q的正上方与Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度正好又变为零,若此电荷在A点处的加速度大小为$\frac{3}{4}$g,试求:
如图所示,Q为固定的正点电荷,A、B两点在Q的正上方与Q相距分别为h和0.25h,将另一点电荷从A点由静止释放,运动到B点时速度正好又变为零,若此电荷在A点处的加速度大小为$\frac{3}{4}$g,试求: