题目内容
20.固定于水平面上的平台,高为h=0.45m,左右两端长度为L=2.133m.一质量为2kg的滑块(可视为质点)置于平台的左端,已知滑块与平台之间的动摩擦因数为0.75,今用大小为16N的拉力作用于滑块上使之由静止开始沿平台向右运动,运动1.8m后撤去拉力,然后滑块继续向前运动,从平台右端水平抛出,落在地面上.回答下列问题(计算结果保留到小数点后2位,重力加速度取g=10m/s2)
(1)拉力F的方向与水平方向成多大角度时,滑块在平台上加速运动阶段的加速度最大?最大加速度为多少?
(2)滑块在平台上运动的最短时间为多少?
(3)滑块落地点距离平台右端最远为多少?
分析 (1)设拉力F的方向与水平方向的角度为θ.根据牛顿第二定律得到加速度a与θ的关系式,再由数学知识求解.
(2)当物体以最大加速度运动时时间最短,由运动学公式求出匀加速运动的时间,再由动能定理求出匀减速运动的末速度,即可由平均速度公式求解出匀减速运动的时间,从而得到总时间.
(3)根据平抛运动的规律求解滑块落地点距离平台右端的距离.
解答  解:(1)设拉力与水平方向成θ角时,加速度为a,则
解:(1)设拉力与水平方向成θ角时,加速度为a,则
Fcosθ-f=ma
N+Fsinθ=mg
又 f=μN
解得:a=$\frac{F(cosθ+μsinθ)}{m}$-μg
由数学知识可知,当θ=arctanμ=37°时加速度最大,为 am=2.5m/s2.
(2)刚撤去F时速度 v1=$\sqrt{2{a}_{m}{s}_{1}}$$\sqrt{2×2.5×1.8}$=3m/s
撤去F后匀减速运动过程,有-μmgs2=$\frac{1}{2}m{v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
式中 s2=L-s1=0.333m
解得:v2=2m/s
所以滑块在平台上运动的最短时间为 tmin=$\frac{{v}_{1}}{{a}_{m}}$+$\frac{{s}_{2}}{\frac{{v}_{1}+{v}_{2}}{2}}$=1.33s
(3)对于平抛过程,有 x=v2t
h=$\frac{1}{2}g{t}^{2}$
解得:x=0.6m
答:
(1)拉力F的方向与水平方向成37°角度时,滑块在平台上加速运动阶段的加速度最大,最大加速度为2.5m/s2.
(2)滑块在平台上运动的最短时间为1.33s.
(3)滑块落地点距离平台右端最远为0.6m.
点评 求极值问题,往往要根据物理规律得到解析式,再由数学知识求解.本题是多过程问题,把握每个过程的规律是解答的关键.

 甲、乙两车在一平直公路上沿同一方向沿直线运动,已知t=0时刻乙车在甲车前面50m,它们的v-t图象如图所示.下列判断正确的是( )
甲、乙两车在一平直公路上沿同一方向沿直线运动,已知t=0时刻乙车在甲车前面50m,它们的v-t图象如图所示.下列判断正确的是( )| A. | 乙车启动时,甲车在其前方50m处 | |
| B. | 运动过程中,乙车落后甲车的最大距离为25m | |
| C. | 乙车启动10s后正好追上甲车 | |
| D. | 乙车超过甲车后,两车还会再相遇 |
 如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )
如图所示为运送粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,(设最大静摩擦力等于滑动摩擦力)以下说法正确的是( )| A. | 粮袋到达B点的速度不可能大于v | |
| B. | 粮袋开始运动的加速度为g(sinθ-μcosθ),若L足够大,则以后将以速度v做匀速运动 | |
| C. | 若μ<tanθ,则粮袋从A到B一直做加速运动 | |
| D. | 不论μ大小如何,粮袋从A到B一直做匀加速运动,且a>gsinθ |

| A. | P受3个力、Q受2个力 | B. | P受3个力、Q受3个力 | ||
| C. | P受4个力、Q受3个力 | D. | P受4个力、Q受4个力 |
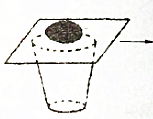 如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )
如图所示,一只杯子固定在水平桌面上,将一块薄纸板盖在杯口并在纸板上放一枚鸡蛋,现用水平向右的拉力将纸板快速抽出,鸡蛋(水平移动距离很小,几乎看不到)掉入杯中,这就是惯性演示.已知鸡蛋(可视为质点)中心离纸板左端的距离为d,鸡蛋和纸板的质量分别为m和2m,所有接触面的动摩擦因数均为μ,重力加速度为g,若鸡蛋移动的距离不超过$\frac{d}{10}$就能保证实验成功,则所需拉力的最小值为( )| A. | 3μmg | B. | 26μmg | C. | 12μmg | D. | 15μmg |
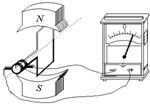
| A. | 指针随着线圈转动而摆动,并且线圈旋转一周,指针左右摆动一次 | |
| B. | 当线圈平面转到跟磁力线垂直的平面位置时,电流表的指针的偏转最大 | |
| C. | 当线圈平面转到跟磁力线平行的位置时,电流表的指针的偏转最大 | |
| D. | 在匀强磁场中匀速转动的线圈里产生感应电动势和感应电流是按正弦规律变化的 |
 如图所示,质量分别为m和2m的A、B两个物块,中间夹着一个被压缩的轻弹簧,A、B两物块被外力制约着静止在水平面上,水平面CD部分是光滑的,其它部分是粗糙的,粗糙部分的动摩擦因数为μ,现同时释放A、B两物块,结果弹簧将两物块弹开,两物块在光滑水平面上滑行一段距离后分别从C点和D点滑上粗糙的水平面,A在粗糙的水平面上滑行的距离为s,求:
如图所示,质量分别为m和2m的A、B两个物块,中间夹着一个被压缩的轻弹簧,A、B两物块被外力制约着静止在水平面上,水平面CD部分是光滑的,其它部分是粗糙的,粗糙部分的动摩擦因数为μ,现同时释放A、B两物块,结果弹簧将两物块弹开,两物块在光滑水平面上滑行一段距离后分别从C点和D点滑上粗糙的水平面,A在粗糙的水平面上滑行的距离为s,求: 光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.
光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑. 如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求
如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求