题目内容
2. 如图所示,在光滑的水平地面上,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,PQ为两个磁场的竖直分界线,磁场范围足够大.一个半径为a、质量为m、电阻为R的金属圆环垂直磁场方向,以速度v从位置I开始向右运动,当圆环运动到位置II(环直径刚好与分界线PQ重合)时,圆环的速度为$\frac{1}{2}v$,则下列说法正确的是( )
如图所示,在光滑的水平地面上,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,PQ为两个磁场的竖直分界线,磁场范围足够大.一个半径为a、质量为m、电阻为R的金属圆环垂直磁场方向,以速度v从位置I开始向右运动,当圆环运动到位置II(环直径刚好与分界线PQ重合)时,圆环的速度为$\frac{1}{2}v$,则下列说法正确的是( )| A. | 圆环运动到位置II时环中有顺时针方向的电流 | |
| B. | 圆环运动到位置II时加速度为$\frac{{4{B^2}{a^2}{v^2}}}{mR}$ | |
| C. | 圆环从位置I运动到位置II的过程中,通过圆环截面的电荷量为$\frac{{πB{a^2}}}{R}$ | |
| D. | 圆环从位置I运动到位置II的过程中,回路产生的电能为$\frac{3}{8}m{v^2}$ |
分析 根据右手定则得出感应电流的方向,根据切割产生的感应电动势公式、欧姆定律以及安培力公式求出圆环所受的合外力,结合牛顿第二定律求出圆环运动的加速度大小.根据q=$\frac{△Φ}{R}$求出通过圆环截面的电荷量.根据能量守恒定律求出回路产生的电能.
解答 解:A、圆环运动到位置II时,根据右手定则知,环中产生顺时针方向的电流,故A正确.
B、圆环运动到位置II时,切割的有效长度为2a,则感应电动势$E=2B•2a•\frac{1}{2}v=2Bav$,电流I=$\frac{E}{R}=\frac{2Bav}{R}$,根据牛顿第二定律得,加速度a=$\frac{2BI•2a}{m}=\frac{8{B}^{2}{a}^{2}v}{mR}$,故B错误.
C、圆环从位置I运动到位置II的过程中,通过圆环截面的电荷量q=$\frac{△Φ}{R}$=$\frac{B•π{a}^{2}}{R}$,故C正确.
D、根据能量守恒知,回路中产生的电能E=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m(\frac{v}{2})^{2}=\frac{3}{8}m{v}^{2}$,故D正确.
故答案为:ACD.
点评 本题考查电磁感应规律、闭合电路运算、感应电动势瞬时值与平均值应用等.关键为:搞清楚磁通量的变化、平动切割的有效长度、瞬时值与平均值,注意求解电量时必须用电流的平均值,不是瞬时值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
16. 如图所示,在光滑的“V”形漏斗中,玻璃球沿水平面做匀速圆周运动,此时小球受到的力有( )
如图所示,在光滑的“V”形漏斗中,玻璃球沿水平面做匀速圆周运动,此时小球受到的力有( )
 如图所示,在光滑的“V”形漏斗中,玻璃球沿水平面做匀速圆周运动,此时小球受到的力有( )
如图所示,在光滑的“V”形漏斗中,玻璃球沿水平面做匀速圆周运动,此时小球受到的力有( )| A. | 重力 | B. | 重力和支持力 | ||
| C. | 重力和向心力 | D. | 重力、支持力和向心力 |
7. 如图所示,边长为a的正方形线框沿光滑的水平面以速度v0进入宽度为L的匀强磁场,a<L,已知线框恰好能穿出磁场,则线框进入磁场和穿出磁场的过程中产生的热量之比Q1:Q2为( )
如图所示,边长为a的正方形线框沿光滑的水平面以速度v0进入宽度为L的匀强磁场,a<L,已知线框恰好能穿出磁场,则线框进入磁场和穿出磁场的过程中产生的热量之比Q1:Q2为( )
 如图所示,边长为a的正方形线框沿光滑的水平面以速度v0进入宽度为L的匀强磁场,a<L,已知线框恰好能穿出磁场,则线框进入磁场和穿出磁场的过程中产生的热量之比Q1:Q2为( )
如图所示,边长为a的正方形线框沿光滑的水平面以速度v0进入宽度为L的匀强磁场,a<L,已知线框恰好能穿出磁场,则线框进入磁场和穿出磁场的过程中产生的热量之比Q1:Q2为( )| A. | 1:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
14.假设地球吸引月球的万有引力在某一瞬时突然消失,月球将( )
| A. | 落到地球表面 | B. | 静止在地球上空某点不动 | ||
| C. | 沿月球轨道切线方向飞出 | D. | 沿月、地连线方向飞出 |
11. 如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两只灯泡的亮度一样,若保持电源电压不变,而将电源频率增大,下列说法正确的是( )
如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两只灯泡的亮度一样,若保持电源电压不变,而将电源频率增大,下列说法正确的是( )
 如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两只灯泡的亮度一样,若保持电源电压不变,而将电源频率增大,下列说法正确的是( )
如图所示,L为电感线圈,C为电容器,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两只灯泡的亮度一样,若保持电源电压不变,而将电源频率增大,下列说法正确的是( )| A. | A灯泡变暗,B灯泡变亮 | B. | A灯泡亮度不变,B灯泡变亮 | ||
| C. | 两灯泡的亮度不变 | D. | A灯泡变亮,B灯泡变暗 |
12.从离地面高为h处,以水平速度v0抛出一物体,物体落地时的速度与竖直方向所成的夹角为θ,取下列四组h和v0的值时,能使θ角最大的一组数据是( )
| A. | h=5m,v0=10m/s | B. | h=10m,v0=6m/s | C. | h=5m,v0=15m/s | D. | h=10m,v0=20m/s |
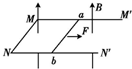 如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦的运动,当棒的运动速度达到某值时框架开始运动,棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g.
如图所示,电阻不计且足够长的U形金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数为μ,框架的宽度为L、质量为m1;质量为m2、电阻为R的均匀导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B.现对导体棒施加一水平恒力F,使棒从静止开始无摩擦的运动,当棒的运动速度达到某值时框架开始运动,棒与框架接触良好,框架与水平面间的最大静摩擦力与滑动摩擦力相等,重力加速度为g. 空间某区域内存在水平方向的匀强磁场,在磁场区域内有两根相距l1=0.8m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示.PM间连接有阻值为R0=1Ω的电阻;QN间连接着两块水平放置的平行金属板a、b,两板相距l2=0.2m.一根电阻为r=3Ω的细导体棒AB,导体棒与导轨接触良好,不计导轨和连接导线的电阻.若导体棒AB以速率v向右匀速运动时,在平行金属板a、b之间有一个带电液滴恰好在竖直平面内以速率v做匀速圆周运动.重力加速度为g,求:
空间某区域内存在水平方向的匀强磁场,在磁场区域内有两根相距l1=0.8m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示.PM间连接有阻值为R0=1Ω的电阻;QN间连接着两块水平放置的平行金属板a、b,两板相距l2=0.2m.一根电阻为r=3Ω的细导体棒AB,导体棒与导轨接触良好,不计导轨和连接导线的电阻.若导体棒AB以速率v向右匀速运动时,在平行金属板a、b之间有一个带电液滴恰好在竖直平面内以速率v做匀速圆周运动.重力加速度为g,求: 如图所示,质量为M的导体棒ab,垂直放在相距为l的平行光滑金属轨道上.导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中.左侧是水平放置、间距为d的平行金属板.R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻.
如图所示,质量为M的导体棒ab,垂直放在相距为l的平行光滑金属轨道上.导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中.左侧是水平放置、间距为d的平行金属板.R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻.