题目内容
5. 如图所示,在宽度分别为a、b的两个区域内分别存在着强度不同,方向相反的匀强磁场,若电子沿垂直于左侧边界线的方向从M点射入磁场,经过两个磁场区域后又沿垂直于右侧边界线从N点射出,电子重力不计,若电子电量和质量分别e和m,电子射入磁场时的速度为V,而M、N两点沿平行于磁场边界的方向上的距离恰为y=$\frac{a+b}{\sqrt{3}}$,则两个区域内磁场的磁感应强度分别为多大?
如图所示,在宽度分别为a、b的两个区域内分别存在着强度不同,方向相反的匀强磁场,若电子沿垂直于左侧边界线的方向从M点射入磁场,经过两个磁场区域后又沿垂直于右侧边界线从N点射出,电子重力不计,若电子电量和质量分别e和m,电子射入磁场时的速度为V,而M、N两点沿平行于磁场边界的方向上的距离恰为y=$\frac{a+b}{\sqrt{3}}$,则两个区域内磁场的磁感应强度分别为多大?
分析 画出粒子运动的轨迹,根据圆的对称性求出其运动轨迹的半径,由牛顿第二定律和向心力公式求出磁感应强度.
解答 解:由于电子能穿越a、b的区域,所以电子在两个区域内偏转的角度都小于90°,结合粒子的圆心的画法,得出其运动的轨迹如图,
由几何关系得:${r}_{1}^{2}={({r}_{1}-\frac{\sqrt{3}}{3}a)}^{2}+{a}^{2}$ ①
${r}_{2}^{2}={({r}_{2}-\frac{\sqrt{3}}{3}b)}^{2}+{b}^{2}$ ②
又由洛伦兹力提供向心力得:$evB=\frac{m{v}^{2}}{r}$ ③
所以:${B}_{1}=\frac{mv}{e{r}_{1}}=\frac{\sqrt{3}mv}{2ea}$
${B}_{2}=\frac{mv}{e{r}_{2}}=\frac{\sqrt{3}mv}{2eb}$
答:两个区域内磁场的磁感应强度分别为$\frac{\sqrt{3}mv}{2ea}$和$\frac{\sqrt{3}mv}{2eb}$.
点评 本题是带电粒子在组合场中运动的问题,解题关键是画出粒子的运动轨迹,运用几何知识求解轨迹半径满足的条件.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15. 如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
 如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )| A. | 光束A为单色光,光束B、C为复色光 | |
| B. | 玻璃对光束C的折射率大于对光束B的折射率 | |
| C. | A、B、C三束光线一定互相平行 | |
| D. | 通过相同的双缝干涉装置,光束B产生的相邻条纹间距要大于光束C产生的相邻亮条纹间距 |
13.物体在下列运动中,机械能守恒的是( )
| A. | 水平匀加速直线运动 | B. | 在斜面上匀速下滑 | ||
| C. | 竖直方向的匀速运动 | D. | 自由落体运动 |
20.一根长L=2m,重力G=200N的均匀木杆放在水平地面上,现将它的一端从地面抬高0.5m,另一端仍搁在地面上,则物体重力势能的变化量为( )
| A. | 50 J | B. | 100 J | C. | 200 J | D. | 400 J |
12. 如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球.当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=90°,质量为m2的小球位于水平地面上,设此时质量为m2的小球对地面压力大小为FN,细线的拉力大小为FT,则( )
如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球.当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=90°,质量为m2的小球位于水平地面上,设此时质量为m2的小球对地面压力大小为FN,细线的拉力大小为FT,则( )
 如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球.当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=90°,质量为m2的小球位于水平地面上,设此时质量为m2的小球对地面压力大小为FN,细线的拉力大小为FT,则( )
如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球.当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=90°,质量为m2的小球位于水平地面上,设此时质量为m2的小球对地面压力大小为FN,细线的拉力大小为FT,则( )| A. | FN=m2g | B. | FN=(m2-m1)g | C. | FT=$\frac{\sqrt{2}}{2}$m1g | D. | FT=(m2-$\frac{\sqrt{2}}{2}$m1)g |
10. 如图所示,在通电密绕长螺线管靠近左端处,吊一金属环a处于静止状态,在其内部也吊一金属环b处于静止状态,两环环面均与螺线管的轴线垂直且环中心恰在螺线管中轴上,当滑动变阻器R的滑片P向左端移动时,a、b两环的运动及变化情况将是( )
如图所示,在通电密绕长螺线管靠近左端处,吊一金属环a处于静止状态,在其内部也吊一金属环b处于静止状态,两环环面均与螺线管的轴线垂直且环中心恰在螺线管中轴上,当滑动变阻器R的滑片P向左端移动时,a、b两环的运动及变化情况将是( )
 如图所示,在通电密绕长螺线管靠近左端处,吊一金属环a处于静止状态,在其内部也吊一金属环b处于静止状态,两环环面均与螺线管的轴线垂直且环中心恰在螺线管中轴上,当滑动变阻器R的滑片P向左端移动时,a、b两环的运动及变化情况将是( )
如图所示,在通电密绕长螺线管靠近左端处,吊一金属环a处于静止状态,在其内部也吊一金属环b处于静止状态,两环环面均与螺线管的轴线垂直且环中心恰在螺线管中轴上,当滑动变阻器R的滑片P向左端移动时,a、b两环的运动及变化情况将是( )| A. | a右摆且有收缩趋势,b左摆且有扩张趋势 | |
| B. | a左摆且有收缩趋势,b右摆且有扩张趋势 | |
| C. | a左摆且有扩张趋势,b不动且有收缩趋势 | |
| D. | a左摆且有收缩趋势,b不动且有扩张趋势 |
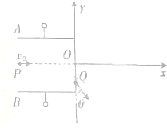 如图所示,在y轴左边有一间距为3d的平行板电容器,两极板的中线PO与x轴重合,上板A带正电.一质量为m、电荷量为q的粒子从板间P点以速度v0射入,从y轴的Q点射出,速度方向与y轴上负方向的夹角θ=30°;在y轴右侧有一半圆形匀强磁场区域磁感应强度的大小B=$\frac{m{v}_{0}}{qd}$,方向垂直纸面向里,粒子经过该磁场区域后能从O点沿x轴负方向回到电场.已知OQ=d,不计粒子重力,求:
如图所示,在y轴左边有一间距为3d的平行板电容器,两极板的中线PO与x轴重合,上板A带正电.一质量为m、电荷量为q的粒子从板间P点以速度v0射入,从y轴的Q点射出,速度方向与y轴上负方向的夹角θ=30°;在y轴右侧有一半圆形匀强磁场区域磁感应强度的大小B=$\frac{m{v}_{0}}{qd}$,方向垂直纸面向里,粒子经过该磁场区域后能从O点沿x轴负方向回到电场.已知OQ=d,不计粒子重力,求: 如图所示,质量为5×10-8kg的带电微粒以V0=2m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长L=10cm,板间距离d=2cm.当UAB=1000V时,带电粒子恰好沿直线穿过板间,则
如图所示,质量为5×10-8kg的带电微粒以V0=2m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长L=10cm,板间距离d=2cm.当UAB=1000V时,带电粒子恰好沿直线穿过板间,则