题目内容
3.在平直轨道上,自行车在汽车前面相距x处以v1=4m/s的速度匀速行驶,汽车则以v2=12m/s的初速度、加速度大小a=2m/s2做匀减速运动.(1)若汽车恰好未追上自行车,则x的大小为多大?
(2)若x=7m,则汽车能追上自行车吗?若能追上,需要多少时间?若后来自行车反过来追上汽车.此时相对汽车的速度为多大?
分析 (1)汽车恰好未追上自行车,计算出汽车减速到和自行车共速的时间,分别求出两车的位移,两车的位移差就两车最初的距离x.
(2)若x=7m,将结果和(1)比较,即可判断汽车能否追上自行车,列出方程,可以求出追上的时间;若后来自行车反过来追上汽车,先判断汽车何时停下,计算出两车的位移,判断出汽车停下时,自行车是否追上了汽车,再分析此时相对汽车的速度.
解答 解:(1)汽车减速时的加速度a=-2m/s2,减速到v1=4m/s所用时间为:
t=$\frac{{v}_{1}-{v}_{2}}{a}=\frac{4-12}{-2}s=4s$
这段时间汽车行驶的位移为:x2=$\frac{{v}_{1}+{v}_{2}}{2}t=\frac{4+12}{2}×4m=32m$
这段时间自行车行驶的位移为:x=v1t=4×4m=16m
故有:x=x2-x1=32m-16m=16m;
(2)若x=7m,小于16m,因此汽车能追上自行车;假设t1时间追上,则有:
${v}_{1}{t}_{1}+x={v}_{2}{t}_{1}+\frac{1}{2}a{t}_{1}^{2}$
解得:t1=1s(另一值7s不符合要求舍去)
汽车追上自行车时,汽车的速度为:
v3=v2+at1=12-2×1=10m/s
若后来自行车反过来追上汽车,则再经过时间t2汽车停下来,即:0=v3+at2
解得:t2=5s
t2时间内,汽车运动的位移为:x3=$\frac{{v}_{3}}{2}{t}_{2}=\frac{10}{2}×5m=25m$
t2时间内,自行车运动的位移为:x4=v1t2=4×5m=20m
由于x4<x3,即汽车停下时,自行车还没有追上汽车
因此后来自行车反过来追上汽车时,此时相对汽车的速度为:v1=4m/s.
答:(1)若汽车恰好未追上自行车,则x的大小为16m.
(2)若x=7m,则汽车能追上自行车,若能追上,需要1s的时间,若后来自行车反过来追上汽车.此时相对汽车的速度4m/s.
点评 本题难度较大,而且比较容易出错,第(1)问要注意:汽车恰好未追上自行车,计算两车距离x时,不是汽车减速到0时,两车的位移差,而是汽车减速到和自行车共速时两者的位移差,因为速度相同还不能追上,那么汽车继续减速就永远追不上自行车.第(2)问计算自行车反过来追上汽车,一定要先考虑汽车何时停下,切不可直接列方程,解出再经过6s自行车追上汽车,这是错误的结论,因为再经过5s汽车就已经停下来了.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案 用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )
用如图所示的装置来验证动量守恒定律.图中PQ为斜槽,QR为水平槽.实验时先将a球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.关于小球落点的下列说法中正确的是( )| A. | 如果小球每一次都从同一点无初速释放,重复几次的落点落在同一位置 | |
| B. | 由于偶然因素存在,重复操作时小球的落点不重合是正常的,但落点应当比较密集 | |
| C. | 测定P点位置时,如果重复10次的落点分别为P1、P2、P3、…P10,则OP应取OP1、OP2、OP3…OP10的平均值,即OP=$\frac{1}{10}$(OP1+OP2+…+OP10的) | |
| D. | 用半径尽量小的圆把P1、P2、P3…P10圈住,这个圆的圆心就是入射球落点的平均位置P |
 如图所示,一条红色光线和另一条紫色光线,以不同的角度同时沿不同的半径方向射入同一块横截面为半圆形玻璃柱体,其透射光线都是由圆心O点沿OC方向射出.则可知( )
如图所示,一条红色光线和另一条紫色光线,以不同的角度同时沿不同的半径方向射入同一块横截面为半圆形玻璃柱体,其透射光线都是由圆心O点沿OC方向射出.则可知( )| A. | BO光线是紫光,OC光线是红光 | |
| B. | 玻璃对BO光线折射率大些 | |
| C. | AO光线较BO光线穿过玻璃砖所需时间长 | |
| D. | 在双缝干涉实验中,若仅将入射光由AO光线变为BO光线,则干涉亮条纹间距变小 |
 质量分别为m1和m2的木块A和B之间用一轻质弹簧相连,然后将它们静置于一底端带有挡板的光滑斜面上,其中B置于斜面底端的挡板上.设斜面的倾角为θ,弹簧的劲度系数为k.现用一平行于斜面的恒力F拉木块A沿斜面由静止开始向上运动,当木块B恰好对挡板的压力为零时,木块A在斜面上运动的速度为v,则下列说法正确的是( )
质量分别为m1和m2的木块A和B之间用一轻质弹簧相连,然后将它们静置于一底端带有挡板的光滑斜面上,其中B置于斜面底端的挡板上.设斜面的倾角为θ,弹簧的劲度系数为k.现用一平行于斜面的恒力F拉木块A沿斜面由静止开始向上运动,当木块B恰好对挡板的压力为零时,木块A在斜面上运动的速度为v,则下列说法正确的是( )| A. | 此时弹簧的弹力大小为m1gsinθ | |
| B. | 拉力F在该过程中对木块A所做的功为$\frac{{(m}_{1}+{m}_{2})gsinθ}{k}$ | |
| C. | 木块A在该过程中重力势能增加了m1$\frac{{(m}_{1}+{m}_{2}){g}^{2}si{n}^{2}θ}{k}$ | |
| D. | 弹簧在该过程中弹性势能增加了$\frac{({m}_{1}{+m}_{2})gsinθ}{k}$-$\frac{1}{2}$mv2 |

| A. | OA段加速度的大小大于在BC段加速度的大小 | |
| B. | OA段质点通过的距离小于在BC段通过的距离 | |
| C. | OA段的运动方向跟BC段运动的方向相反 | |
| D. | OA段加速度的方向跟在BC段加速度的方向相反 |
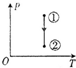
 如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )
如图所示,内壁光滑的导热气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸中.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②.如果环境保持恒温,则下图中可表示此过程的图象是( )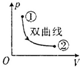


 如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.
如图所示,固定的光滑圆弧轨道ACB的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m.物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2. 水平放置的金属框架abcd,宽度为0.5m,匀强磁场与框架平面成45°角,如图所示,磁感应强度为1.0T,框架电阻不计.金属杆MN置于框架上可以无摩擦地滑动,MN的量0.5kg,电阻0.25Ω,当用水平恒力F拉着MN水平匀速运动时.它对框架的压力恰为零.求:
水平放置的金属框架abcd,宽度为0.5m,匀强磁场与框架平面成45°角,如图所示,磁感应强度为1.0T,框架电阻不计.金属杆MN置于框架上可以无摩擦地滑动,MN的量0.5kg,电阻0.25Ω,当用水平恒力F拉着MN水平匀速运动时.它对框架的压力恰为零.求: