题目内容
8. 要发射一颗人造地球卫星,使它在半径为r2的预定轨道上绕地球做匀速圆周运动,为此先将卫星发射到半径为r1的近地暂行轨道上绕地球做匀速圆周运动.如图所示,在A点,使卫星速度瞬时增加,从而使卫星进入一个椭圆的转移轨道上,当卫星到达转移轨道的远地点B时,再次瞬时改变卫星速度,使它进入预定轨道运行.已知地球表面的重力加速度大小为g,地球的半径为R,则卫星在半径为r1的近地暂行轨道上的运动周期为$T=2π\sqrt{\frac{{{r}_{1}}^{3}}{GM}}$,卫星从半径为r1的近地暂行轨道上的A点转移到半径为r2的预定轨道上的B点所需时间为$\frac{π({r}_{1}+{r}_{2})}{2R}\sqrt{\frac{{r}_{1}+{r}_{2}}{2g}}$.
要发射一颗人造地球卫星,使它在半径为r2的预定轨道上绕地球做匀速圆周运动,为此先将卫星发射到半径为r1的近地暂行轨道上绕地球做匀速圆周运动.如图所示,在A点,使卫星速度瞬时增加,从而使卫星进入一个椭圆的转移轨道上,当卫星到达转移轨道的远地点B时,再次瞬时改变卫星速度,使它进入预定轨道运行.已知地球表面的重力加速度大小为g,地球的半径为R,则卫星在半径为r1的近地暂行轨道上的运动周期为$T=2π\sqrt{\frac{{{r}_{1}}^{3}}{GM}}$,卫星从半径为r1的近地暂行轨道上的A点转移到半径为r2的预定轨道上的B点所需时间为$\frac{π({r}_{1}+{r}_{2})}{2R}\sqrt{\frac{{r}_{1}+{r}_{2}}{2g}}$.
分析 (1)根据万有引力提供向心力求解.
(2)根据卫星的运动图形和几何关系,确定出椭圆轨道的半长轴a,再利用开普勒第三定律求解.
解答 解:(1)卫星在近地暂行轨道上运行所需要的向心力由万有引力提供$G\frac{Mm}{{{r}_{1}}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}{r}_{1}$,得$T=2π\sqrt{\frac{{{r}_{1}}^{3}}{GM}}$
在地球表面上的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$,得GM=R2g
所以$T=2π\sqrt{\frac{{{r}_{1}}^{3}}{{R}^{2}g}}$=$\frac{2π{r}_{1}}{R}\sqrt{\frac{{r}_{1}}{g}}$
(2)设卫星预定轨道半径为r,当卫星在转移轨道运行,其半长轴为:a=$\frac{{r}_{1}+{r}_{2}}{2}$
根据开普勒第三定律得:$\frac{{{r}_{1}}^{3}}{{T}^{2}}=\frac{{a}^{3}}{(2t)^{2}}$
化简得$(2t)^{2}=(\frac{\frac{{r}_{1}+{r}_{2}}{2}}{{r}_{1}})^{3}T$
解得:$t=\frac{{r}_{1}+{r}_{2}}{4{r}_{1}}\sqrt{\frac{{r}_{1}+{r}_{2}}{2{r}_{1}}}•T$
代入T值,得$t=\frac{{r}_{1}+{r}_{2}}{4{r}_{1}}\sqrt{\frac{{r}_{1}+{r}_{2}}{2{r}_{1}}}•\frac{2π{r}_{1}}{R}\sqrt{\frac{{r}_{1}}{g}}$=$\frac{π({r}_{1}+{r}_{2})}{2R}\sqrt{\frac{{r}_{1}+{r}_{2}}{2g}}$
故答案为:$T=2π\sqrt{\frac{{{r}_{1}}^{3}}{GM}}$;$\frac{π({r}_{1}+{r}_{2})}{2R}\sqrt{\frac{{r}_{1}+{r}_{2}}{2g}}$.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力两知识点,以及会用开普勒第三定律解题.

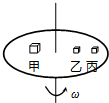 如图所示,甲、乙、丙三个物体放在匀速转动的水平粗糙圆台上,甲的质量为2m,乙、丙的质量均为m,甲、乙离转轴的距离为R,丙离转轴的距离为2R,则当圆台旋转时(设甲、乙、丙始终与圆台保持相对静止)( )
如图所示,甲、乙、丙三个物体放在匀速转动的水平粗糙圆台上,甲的质量为2m,乙、丙的质量均为m,甲、乙离转轴的距离为R,丙离转轴的距离为2R,则当圆台旋转时(设甲、乙、丙始终与圆台保持相对静止)( )| A. | 甲物体的线速度比丙物体的线速度小 | |
| B. | 乙物体的角速度比丙物体的角速度小 | |
| C. | 甲物体的向心加速度比乙物体的向心加速度大 | |
| D. | 乙物体受到的向心力比丙物体受到的向心力小 |
 如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )
如图,足够长的U型光滑金属导轨平面与水平面成θ角(0<θ<90°),其中MN与PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电量为q时,它的速度大小为v,则金属棒ab在这一过程中( )| A. | F运动的平均速度大小为$\frac{1}{2}$v | |
| B. | 平滑位移大小为$\frac{qR}{BL}$ | |
| C. | 产生的焦耳热为mgsinθ-mv2 | |
| D. | 受到的最大安培力大小为$\frac{{B}^{2}{L}^{2}v}{R}$sinθ |

| A. | 斜劈A对地向右运动 | B. | 斜劈A受到地面向右的摩擦力作用 | ||
| C. | 斜劈A对地面的压力大小等于(M+2m)g | D. | 斜劈A对地面的压力大于(M+2m)g |
| A. | 增大 | B. | 减少 | C. | 不变 | D. | 不能判定 |
 如图所示,带电的平行金属板电容器水平放置,质量相同、重力不计的带电微粒A、B,平行于极板以相同的初速度射入电场,结果打在极板上的同一点P.不计两微粒之间的相互作用,下列说法正确的是( )
如图所示,带电的平行金属板电容器水平放置,质量相同、重力不计的带电微粒A、B,平行于极板以相同的初速度射入电场,结果打在极板上的同一点P.不计两微粒之间的相互作用,下列说法正确的是( )| A. | 在电场中微粒A运动的时间比B长 | B. | 微粒A所带的电荷量比B多 | ||
| C. | 电场力对微粒A做的功比B少 | D. | 到达P点时微粒A的速率比B小 |
| A. | k=$\frac{1}{2}$ | B. | k=2 | C. | n=$\frac{1}{\sqrt{5}}$ | D. | n=$\sqrt{5}$ |
 如图所示,实线为一簇未标明方向的点电荷Q周围的电场线,若带电粒子q(|Q|远大于|q|)由a运动到b,电场力做正功;粒子在a、b两点所受电场力分别为Fa、Fb,则下列判断正确的是( )
如图所示,实线为一簇未标明方向的点电荷Q周围的电场线,若带电粒子q(|Q|远大于|q|)由a运动到b,电场力做正功;粒子在a、b两点所受电场力分别为Fa、Fb,则下列判断正确的是( )| A. | 若Q为正电荷,则q带正电,Fa>Fb | B. | 若Q为正电荷,则q带负电,Fa<Fb | ||
| C. | 若Q为负电荷,则q带正电,Fa>Fb | D. | 若Q为负电荷,则q带负电,Fa<Fb |
 2011年8月,“嫦娥二号”成功进入环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.若除去图中的“日地拉格朗日点”外,则在“日-地”连线上具有上述功能的点的个数为( )
2011年8月,“嫦娥二号”成功进入环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动.若除去图中的“日地拉格朗日点”外,则在“日-地”连线上具有上述功能的点的个数为( )