题目内容
8.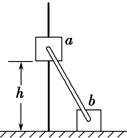 如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.
如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.(1)画出当a即将落地前(杆尚未转至水平方向)滑块a、b的受力分析图;
(2)求当a的机械能最小时,地面对b支持力的大小(要有过程分析);
(3)求a落地时速度的大小.
分析 (1)分别以a、b为研究对象,进行受力分析,画出受力图即可;
(2)当a落地前b的加速度为零,即轻杆对b的作用力为零时,b的机械能最大,a的机械能最小由此即可得出结论;
(3)a、b组成的系统只有重力做功,系统机械能守恒,通过b的动能变化,判断轻杆对b的做功情况.根据系统机械能守恒求出a球运动到最低点时的速度大小.
解答  解:(1)受力分析如图所示
解:(1)受力分析如图所示
(2)过程分析:当a刚落地时,b的速度为零.当a落地前b的加速度为零,即轻杆对b的作用力为零时,b的机械能最大,a的机械能最小,这时b受重力、支持力.
即FNb=mg
(3)以滑块a、b及轻杆组成的系统为研究对象,系统的机械能守恒,
则mgh=$\frac{1}{2}$mva2+0,即va=$\sqrt{2gh}$
答:(1)画出当a即将落地前(杆尚未转至水平方向)滑块a、b的受力分析图如图;
(2)当a的机械能最小时,地面对b支持力的大小是mg;
(3)a落地时速度的大小是$\sqrt{2gh}$.
点评 解决本题的关键知道a、b组成的系统机械能守恒,以及知道当a的机械能最小时,b的动能最大.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18. 如图为表演杂技“飞车走壁”的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的摩擦,下列说法中正确的是( )
如图为表演杂技“飞车走壁”的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的摩擦,下列说法中正确的是( )
 如图为表演杂技“飞车走壁”的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的摩擦,下列说法中正确的是( )
如图为表演杂技“飞车走壁”的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的摩擦,下列说法中正确的是( )| A. | 在a轨道上运动时角速度较大 | |
| B. | 在a轨道上运动时线速度较大 | |
| C. | 在a、b两轨道上运动时摩托车对侧壁的压力相等 | |
| D. | 在a轨道上运动时摩托车和运动员所受的向心力较大 |
19. 如图所示,物体B被钉牢在放于光滑水平地面的平板小车上,物体A以速率v沿水平粗糙车板向着B运动并发生碰撞.则( )
如图所示,物体B被钉牢在放于光滑水平地面的平板小车上,物体A以速率v沿水平粗糙车板向着B运动并发生碰撞.则( )
 如图所示,物体B被钉牢在放于光滑水平地面的平板小车上,物体A以速率v沿水平粗糙车板向着B运动并发生碰撞.则( )
如图所示,物体B被钉牢在放于光滑水平地面的平板小车上,物体A以速率v沿水平粗糙车板向着B运动并发生碰撞.则( )| A. | 对于A与B组成的系统动量守恒 | |
| B. | 对于A与小车组成的系统动量守恒 | |
| C. | 对于A、B与小车组成的系统动量守恒 | |
| D. | 以上说法都不对 |
13.两个点电荷相距r时,相互作用力为F,则( )
| A. | 两电荷量都不变距离加倍时,作用力变为$\frac{F}{4}$ | |
| B. | 其中一个电荷的电荷量和两电荷间距都减半时,作用力不变 | |
| C. | 每个电荷的电荷量和两电荷间距都减半时,作用力为4F | |
| D. | 两个电荷的电荷量和两电荷间距都增加相同倍数时,作用力不变 |
20.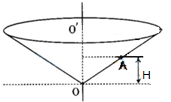 如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
 如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )| A. | $\sqrt{\frac{g}{2H}}$ | B. | $\sqrt{\frac{5g}{8H}}$ | C. | $\sqrt{\frac{3g}{2H}}$ | D. | $\sqrt{\frac{2g}{H}}$ |
12. 甲、乙两物体在同一直线上,同时由同一位置同一方向做直线运动,其速度与时间的函数图象如图所示,下列说法中正确的是( )
甲、乙两物体在同一直线上,同时由同一位置同一方向做直线运动,其速度与时间的函数图象如图所示,下列说法中正确的是( )
 甲、乙两物体在同一直线上,同时由同一位置同一方向做直线运动,其速度与时间的函数图象如图所示,下列说法中正确的是( )
甲、乙两物体在同一直线上,同时由同一位置同一方向做直线运动,其速度与时间的函数图象如图所示,下列说法中正确的是( )| A. | 开始阶段乙运动在甲在前面,20 s后乙落在甲的后面 | |
| B. | 第20 s末乙追上甲,且甲、乙运动速度相等 | |
| C. | 第40 s末乙追上甲 | |
| D. | 第40 s末,两物体相距最大 |
 (1)在“验证机械能守恒定律”的实验中,有如下器材:
(1)在“验证机械能守恒定律”的实验中,有如下器材: 为了测定一节干电池的电动势和内阻,实验室提供了下列器材:
为了测定一节干电池的电动势和内阻,实验室提供了下列器材: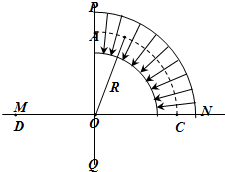 如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场.
如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场.