题目内容
14. 如图所示,两根长度不同的细线的上端固定在天花板上的同一点,下端分别系一小球.现使两个小球在同一水平面内作匀速圆周运动,关于两小球的受力和运动情况,下列说法中正确的是( )
如图所示,两根长度不同的细线的上端固定在天花板上的同一点,下端分别系一小球.现使两个小球在同一水平面内作匀速圆周运动,关于两小球的受力和运动情况,下列说法中正确的是( )| A. | 受到细线拉力的大小一定相等 | B. | 线速度的大小一定相等 | ||
| C. | 运动的周期一定相等 | D. | 向心加速度的大小一定相等 |
分析 两个小球均做匀速圆周运动,对它们受力分析,找出向心力来源,可先求出角速度,再由角速度与线速度、周期、向心加速度的关系公式求解
解答 解:对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;
将重力与拉力合成,合力指向圆心,由几何关系得,合力:F=mgtanθ…①;
绳子拉力T=$\frac{mg}{cosθ}$,不知两小球质量情况,故A错误
由向心力公式得:F=mω2r…②;
设球与悬挂点间的高度差为h,由几何关系,得:r=htanθ…③;
由①②③三式得,ω=$\sqrt{\frac{g}{h}}$,与绳子的长度和转动半径无关,又由T=$\frac{2π}{ω}$,故C正确;
由v=wr,两球转动半径不等,故B错误;
由a=ω2r,两球转动半径不等,故D错误;
故选:C
点评 本题关键要对球受力分析,找向心力来源,求角速度;同时要灵活应用角速度与线速度、周期、向心加速度之间的关系公式!

练习册系列答案
相关题目
4. 木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示.假设木块与地面之间的最大静摩擦力等于二者之间的滑动摩擦力,则力F作用后( )
木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示.假设木块与地面之间的最大静摩擦力等于二者之间的滑动摩擦力,则力F作用后( )
 木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示.假设木块与地面之间的最大静摩擦力等于二者之间的滑动摩擦力,则力F作用后( )
木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示.假设木块与地面之间的最大静摩擦力等于二者之间的滑动摩擦力,则力F作用后( )| A. | 木块A所受摩擦力大小是12.5N | B. | 木块A所受摩擦力大小是11.5N | ||
| C. | 木块B所受摩擦力大小是9N | D. | 木块B所受摩擦力大小是7N |
2. 如图所示,轻杆一头P用光滑轴固定于竖直墙壁上(杆可绕P点转动),另一头O用轻绳悬挂于墙上A点,一物体被悬挂于O点,杆恰好水平.现在将墙上绳的悬挂点上移,同时加长轻绳使杆仍保持水平,则关于轻杆受压力与轻绳受拉力的下列说法正确的是( )
如图所示,轻杆一头P用光滑轴固定于竖直墙壁上(杆可绕P点转动),另一头O用轻绳悬挂于墙上A点,一物体被悬挂于O点,杆恰好水平.现在将墙上绳的悬挂点上移,同时加长轻绳使杆仍保持水平,则关于轻杆受压力与轻绳受拉力的下列说法正确的是( )
 如图所示,轻杆一头P用光滑轴固定于竖直墙壁上(杆可绕P点转动),另一头O用轻绳悬挂于墙上A点,一物体被悬挂于O点,杆恰好水平.现在将墙上绳的悬挂点上移,同时加长轻绳使杆仍保持水平,则关于轻杆受压力与轻绳受拉力的下列说法正确的是( )
如图所示,轻杆一头P用光滑轴固定于竖直墙壁上(杆可绕P点转动),另一头O用轻绳悬挂于墙上A点,一物体被悬挂于O点,杆恰好水平.现在将墙上绳的悬挂点上移,同时加长轻绳使杆仍保持水平,则关于轻杆受压力与轻绳受拉力的下列说法正确的是( )| A. | 二者均减小 | B. | 二者均增大 | ||
| C. | 轻杆受压力增大,轻绳受拉力减小 | D. | 轻杆受压力减小,轻绳受拉力增大 |
9. 如图所示,a、b是两个相同的小灯泡,L是一个自感系数很大的线圈,其直流电阻值与R相同,且R小于小灯泡的电阻.闭合开关S待电路达到稳定后,a、b两灯泡均可发光.由于自感作用,在开关S接通和断开后,灯泡a和b的发光情况是( )
如图所示,a、b是两个相同的小灯泡,L是一个自感系数很大的线圈,其直流电阻值与R相同,且R小于小灯泡的电阻.闭合开关S待电路达到稳定后,a、b两灯泡均可发光.由于自感作用,在开关S接通和断开后,灯泡a和b的发光情况是( )
 如图所示,a、b是两个相同的小灯泡,L是一个自感系数很大的线圈,其直流电阻值与R相同,且R小于小灯泡的电阻.闭合开关S待电路达到稳定后,a、b两灯泡均可发光.由于自感作用,在开关S接通和断开后,灯泡a和b的发光情况是( )
如图所示,a、b是两个相同的小灯泡,L是一个自感系数很大的线圈,其直流电阻值与R相同,且R小于小灯泡的电阻.闭合开关S待电路达到稳定后,a、b两灯泡均可发光.由于自感作用,在开关S接通和断开后,灯泡a和b的发光情况是( )| A. | S接通时灯a先达到最亮,S断开时灯a后暗 | |
| B. | S接通时灯a先达到最亮,S断开时灯b后暗 | |
| C. | S接通时灯b先达到最亮,S断开时灯a后暗 | |
| D. | S接通时灯b先达到最亮,S断开时灯b后暗 |
6.光滑水平面上放置两个等量同种电荷,其连线中垂线上有A、B、C三点,如图甲所示.一个质量m=1kg的小物块(可视为质点)自C点由静止释放,小物块带电量q=2C,其运动的v-t图线如图乙所示,其中B点为整条图线切线斜率最大位置(图中标出了该切线),下列判断正确的是( )
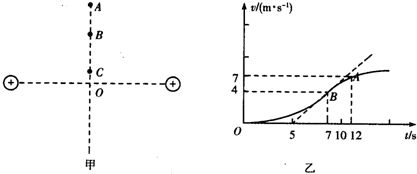

| A. | 由C点到A点,电势逐渐降低 | |
| B. | B、A两点间的电势差为UBA=8.25V | |
| C. | 由C点到A点物块的电势能先减小后变大 | |
| D. | B点为中垂线上电场强度最大的点,场强E=1V/m |

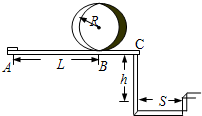 某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5W工作,进入竖直圆轨道前受到的阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m.
某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5W工作,进入竖直圆轨道前受到的阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m.
 某同学利用图的实验装置测量重力加速度.测量滑块在运动过程中所受的合外力是“探究动能定理”实验要解决的一个重要问题.
某同学利用图的实验装置测量重力加速度.测量滑块在运动过程中所受的合外力是“探究动能定理”实验要解决的一个重要问题.