题目内容
13.我们通常把周期为2秒的单摆称为“秒摆”,请你计算秒摆的摆长是多少?根据你所学过的物理知识,证明秒摆在竖直平面内小幅度摆动时做简谐运动.分析 由单摆的周期公式$T=2π\sqrt{\frac{l}{g}}$可求得单摆的摆长;根据摆球的受力,结合简谐振动的条件即可证明.
解答 解:周期为2s;由单摆的周期公式$T=2π\sqrt{\frac{l}{g}}$可得:L=$\frac{g{T}^{2}}{4{π}^{2}}=\frac{9.8×{2}^{2}}{2×3.1{4}^{2}}≈1$m
单摆在振动中重力沿切向的分力是单摆简谐运动的回复力,在角度很小的情况下:$sinθ≈θ=\frac{s}{L}≈\frac{x}{L}$,
所以:${F_回}=mgsinθ≈\frac{mgx}{L}$回复力的方向跟位移方向相反
即回复力的大小跟偏离平衡位置的距离成正比,受力的方向跟位移的方向相反,所以是简谐运动.
答:秒摆的摆长是1m;证明同上.
点评 解决本题的关键掌握单摆的周期公式$T=2π\sqrt{\frac{l}{g}}$,简单.

练习册系列答案
相关题目
5.做匀速圆周运动的物体,发生变化的物理量是( )
| A. | 速度 | B. | 动能 | C. | 角速度 | D. | 周期 |
1. 如图所示,一平行导轨水平放置,距为d,一端连接电阻R,磁场的磁感应强度为B,方向与导轨所在平面垂直.一根光滑金属棒ab与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿平行于导轨的方向以速度v匀速滑行时,则作用于金属棒的拉力的大小与方向是( )
如图所示,一平行导轨水平放置,距为d,一端连接电阻R,磁场的磁感应强度为B,方向与导轨所在平面垂直.一根光滑金属棒ab与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿平行于导轨的方向以速度v匀速滑行时,则作用于金属棒的拉力的大小与方向是( )
 如图所示,一平行导轨水平放置,距为d,一端连接电阻R,磁场的磁感应强度为B,方向与导轨所在平面垂直.一根光滑金属棒ab与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿平行于导轨的方向以速度v匀速滑行时,则作用于金属棒的拉力的大小与方向是( )
如图所示,一平行导轨水平放置,距为d,一端连接电阻R,磁场的磁感应强度为B,方向与导轨所在平面垂直.一根光滑金属棒ab与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿平行于导轨的方向以速度v匀速滑行时,则作用于金属棒的拉力的大小与方向是( )| A. | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{R}$,方向是水平向右 | |
| B. | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{R}$,方向是垂直金属棒斜向下 | |
| C. | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{Rsinθ}$,方向是垂直金属棒斜向下 | |
| D. | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{Rsinθ}$,方向是水平向右 |
5.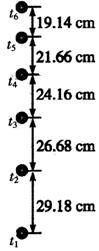 某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
(1)根据频闪照片上的数据计算t5时刻小球的速度v5=4.08m/s;
(2)从t2时刻到t5时刻,小球重力势能的增加量△Ep=1.45J,动能的减少量△Ek=1.46J. 在误差允许的范围内,若△Ep与△Ek近似相等,就能验证机械能守恒定律.(以上结果均保留三位有效数字)
 某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:
某同学利用频闪照相法验证机械能守恒定律.该同学将一质量为m=0.2kg的小球竖直上抛,获得部分运动过程的频闪照片如图所示.已知图中所标数据为实际距离,频闪仪每隔0.05s闪光一次,当地重力加速度为10m/s2.该同学通过计算得到不同时刻的速度如下表:| 时刻 | t2 | t3 | t4 | t5 |
| 速度(m/s) | 5.59 | 5.08 | 4.58 |
(2)从t2时刻到t5时刻,小球重力势能的增加量△Ep=1.45J,动能的减少量△Ek=1.46J. 在误差允许的范围内,若△Ep与△Ek近似相等,就能验证机械能守恒定律.(以上结果均保留三位有效数字)
2. 静止在水平地面的物块,受到水平向右的拉力F的作用,F随时间t的变化情况如图所示.设物块与地面间的最大静摩擦力与滑动摩擦力大小相等,且为1N,则( )
静止在水平地面的物块,受到水平向右的拉力F的作用,F随时间t的变化情况如图所示.设物块与地面间的最大静摩擦力与滑动摩擦力大小相等,且为1N,则( )
 静止在水平地面的物块,受到水平向右的拉力F的作用,F随时间t的变化情况如图所示.设物块与地面间的最大静摩擦力与滑动摩擦力大小相等,且为1N,则( )
静止在水平地面的物块,受到水平向右的拉力F的作用,F随时间t的变化情况如图所示.设物块与地面间的最大静摩擦力与滑动摩擦力大小相等,且为1N,则( )| A. | 0~1s时间内,物块的加速度逐渐增大 | |
| B. | 第3s末,物块的速度最大 | |
| C. | 第3s末,物块的加速度为零 | |
| D. | 第7s末,物块的动能最大 |
 如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L=0.50m,导轨平面与水平面夹角为α=37°,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B=0.40T.金属导轨的上端与开关S,阻值为R1的定值电阻和电阻箱R2相连,不计一切摩擦,不计导轨、金属棒的电阻.现在闭合开关S,将金属棒由静止释放,金属棒能达到的最大速度vm随电阻箱R2阻值的变化关系如图乙所示.重力加速度为g取10m/s2,sin 37°=0.60,cos 37°=0.80.求R1的大小和金属棒的质量m.
如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L=0.50m,导轨平面与水平面夹角为α=37°,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B=0.40T.金属导轨的上端与开关S,阻值为R1的定值电阻和电阻箱R2相连,不计一切摩擦,不计导轨、金属棒的电阻.现在闭合开关S,将金属棒由静止释放,金属棒能达到的最大速度vm随电阻箱R2阻值的变化关系如图乙所示.重力加速度为g取10m/s2,sin 37°=0.60,cos 37°=0.80.求R1的大小和金属棒的质量m. 如图所示,底边在x轴上,长为3L,高为L,底角为45°的等腰梯形内分布着垂直纸面向外的匀强磁场.t=0时有一边长也为L的正方形导线框恰好位于图示位置沿x轴正方向匀速穿过该磁场区域.若以顺时针方向为导线框中电流的正方向,在下面四幅图中能正确表示导线框中电流和位移关系的是( )
如图所示,底边在x轴上,长为3L,高为L,底角为45°的等腰梯形内分布着垂直纸面向外的匀强磁场.t=0时有一边长也为L的正方形导线框恰好位于图示位置沿x轴正方向匀速穿过该磁场区域.若以顺时针方向为导线框中电流的正方向,在下面四幅图中能正确表示导线框中电流和位移关系的是( )



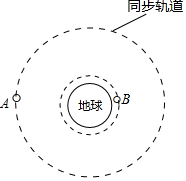 如图所示,A是地球同步卫星,B是近地卫星,它们的轨道半径之比为6:1
如图所示,A是地球同步卫星,B是近地卫星,它们的轨道半径之比为6:1