题目内容
14. 从地面上以初速度v0=10m/s竖直向上抛出一质量为m=0.2kg的小球,若运动过程中小球受到的空气阻力f与其速率v成正比,其关系为f=kv,小球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1=2m/s,且落地前已经做匀速运动(取g=10m/s2),则以下说法正确的是( )
从地面上以初速度v0=10m/s竖直向上抛出一质量为m=0.2kg的小球,若运动过程中小球受到的空气阻力f与其速率v成正比,其关系为f=kv,小球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1=2m/s,且落地前已经做匀速运动(取g=10m/s2),则以下说法正确的是( )| A. | k的值为1kg•s/m | |
| B. | 小球在上升阶段速度大小为1 m/s时,加速度大小为20 m/s2 | |
| C. | 小球抛出瞬间的加速度大小为60 m/s2 | |
| D. | 小球抛出到落地过程中所用时间为1.2s |
分析 根据落地前做匀速运动,由平衡条件求出比例系数k.根据牛顿第二定律研究加速度大小为20 m/s2时的速度大小.根据牛顿第二定律求出抛出瞬间的加速度大小;上升时根据牛顿第二定律(mg+kv)=ma可计算加速度a,取极短△t时间,速度变化△v,有:△v=a△t,上升全程∑△v=0-v0=∑a△t,下降过程,运用同样的方法求出从最高点落回到地面所用的时间.
解答 解:A、小球落地前以v1匀速运动,则有mg=kv1,即k=$\frac{mg}{{v}_{1}}=\frac{0.2×10}{2}$N•s/m=1N•s/m,A选项给出的单位错误,所以A错误;
B、小球在上升阶段速度大小为1m/s时,根据牛顿第二定律得:mg+kv=ma,解得:a=当a=20m/s2时,得 v=$g+\frac{kv}{m}=(10+\frac{1×1}{0.2})m/{s}^{2}$=15m/s2,B错误;
C、小球抛出瞬间的加速度大小a=$g+\frac{k{v}_{0}}{m}=(10+\frac{1×10}{0.2})m/{s}^{2}$=60 m/s2,故C正确;
D、上升时加速度为a,上升的最大高度为H,根据牛顿第二定律可得:mg+kv=ma;
取极短时间△t内,速度变化△v,有:mg△t+kv△t=ma△t=m△v,
上升的全过程:mg•∑△t+k•∑△v=m•∑△v,
又:∑v△t=∑△h=H,∑△v=0-(-v0)=v0,
解得:mgt1+kH=mv0;
下降时加速度为a2,mg-kv=ma2,
同理可得:mg△t-kv△t=ma2△t=m△v,
所以:mgt2-kH=mv1,
解得:t1+t2=$\frac{{v}_{0}+{v}_{1}}{g}=\frac{12}{10}s=1.2s$,所以D正确.
故选:CD.
点评 本题是信息给予题,要把握空气阻力与速率的关系,注意空气阻力方向与运动方向相反,一直做负功.运用动能定理和牛顿运动定律进行研究.在运用动量定理解题注意要合理地选择研究的过程.

 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0,点A处的电势为6V,点B处的电势为3V,则该电场的场强是( )
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0,点A处的电势为6V,点B处的电势为3V,则该电场的场强是( )| A. | 方向与y轴负方向的夹角为30° | B. | 方向与y轴负方向的夹角为60° | ||
| C. | 大小为200$\sqrt{3}$V/m | D. | 大小为200V/m |
 如图所示,甲乙两个完全相同的车静止在水平面上,其中一个车内有人,此人拉动轻绳使两车相互靠近,相遇时甲乙两车距离出发点分别为S甲和S乙.下列判断正确的是( )
如图所示,甲乙两个完全相同的车静止在水平面上,其中一个车内有人,此人拉动轻绳使两车相互靠近,相遇时甲乙两车距离出发点分别为S甲和S乙.下列判断正确的是( )| A. | 若车与轨道间无摩擦,则S甲=S乙 | |
| B. | 若车与轨道间有摩擦,且S甲<S乙,则人在甲车内 | |
| C. | 若S甲<S乙,且人在甲车内,则车与轨道可能无摩擦 | |
| D. | 只要S甲<S乙,则人一定在甲车内 |
 如图所示,在光滑的水平地面上,质量为m1的物块和质量为m2的小球通过轻弹簧连接,在力F的作用下一起沿水平方向做匀加速运动(物块在地面上,小球在空中),已知力F与水平方向的夹角为θ,则下列说法正确的是( )
如图所示,在光滑的水平地面上,质量为m1的物块和质量为m2的小球通过轻弹簧连接,在力F的作用下一起沿水平方向做匀加速运动(物块在地面上,小球在空中),已知力F与水平方向的夹角为θ,则下列说法正确的是( )| A. | 物块的加速度为$\frac{Fcosθ}{{m}_{1}+{m}_{2}}$ | |
| B. | 物块受到地面的支持力大小为m1g-Fsinθ | |
| C. | 弹簧的弹力大小等于拉力F和小球重力的合力 | |
| D. | 如果在物块上再固定一个质量为m1的物体,则它们的加速度不变 |
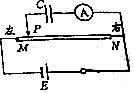 如图所示,E为内阻不计的电源,MN为同种材料制成的粗细均匀的长电阻丝,C为电容器.当滑动触头P以恒定速率从左向右匀速滑动时,关于电流计A的读数情况及通过A的电流方向.下列说法正确的是( )
如图所示,E为内阻不计的电源,MN为同种材料制成的粗细均匀的长电阻丝,C为电容器.当滑动触头P以恒定速率从左向右匀速滑动时,关于电流计A的读数情况及通过A的电流方向.下列说法正确的是( )| A. | 读数逐渐变小.通过A的电流方向向左 | |
| B. | 读数逐渐变大,通过A的电流方向向右 | |
| C. | 读数稳定,通过A的电流方向向右 | |
| D. | 读数稳定,通过A的电流方向向左 |
 如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=lkg的小球,小球左侧连接一水平轻弹簧,弹簧左端固定在墙上,右侧连接一与竖直方向成θ=45°角的不可伸长的轻绳,轻绳另一端固定在天花板上,此时小球处于静止状态,且水平面对小球的弹力恰好为零.在剪断轻绳的瞬间(g取10m/s2),下列说法中正确的是( )
如图所示,在动摩擦因数μ=0.2的水平面上有一个质量m=lkg的小球,小球左侧连接一水平轻弹簧,弹簧左端固定在墙上,右侧连接一与竖直方向成θ=45°角的不可伸长的轻绳,轻绳另一端固定在天花板上,此时小球处于静止状态,且水平面对小球的弹力恰好为零.在剪断轻绳的瞬间(g取10m/s2),下列说法中正确的是( )| A. | 小球受力个数不变 | |
| B. | 小球立即向左加速,且加速度的大小为a=8m/s2 | |
| C. | 小球立即向左加速,且加速度的大小为a=l0m/s2 | |
| D. | 若剪断的是弹簧,则剪断瞬间小球加速度的大小a=l0$\sqrt{2}$m/s2 |
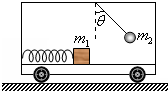 在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.
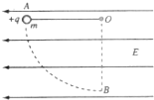 如图所示,空间某区域存在水平方向的匀强电场E=2×104N/C,将一长为L=500cm的不可伸长的绝缘细线一端固定于O点,另一端连接一个质量为m=0.5kg的小球(可视为质点),小球带电量q=1.6×10-4C,现将绝缘细线AO拉至与电场线平行位置,且细线刚好拉直,让小球从A处静止释放,取g=10m/s2,求:
如图所示,空间某区域存在水平方向的匀强电场E=2×104N/C,将一长为L=500cm的不可伸长的绝缘细线一端固定于O点,另一端连接一个质量为m=0.5kg的小球(可视为质点),小球带电量q=1.6×10-4C,现将绝缘细线AO拉至与电场线平行位置,且细线刚好拉直,让小球从A处静止释放,取g=10m/s2,求: