题目内容
一足够长的竖直圆筒，质量为m=2kg的小球恰能放入圆筒中，小球只要在圆筒内就能受到一竖直向上的作用恒力F=23N，最初小球在圆筒的底部且静止．现让圆筒以速度V=4m/s水平向右匀速运动2s．重力加速度g=10m/s2．求：（1）此过程中小球的机械能改变量；
（2）2s时小球的位移和速度．
【答案】分析：（1）小球在玻璃管与恒力共同作用下做类平抛运动，水平方向做匀速直线运动，竖直方向向下做初速度为零的匀加速直线运动．小球在运动过程中，除重力做功外，还有恒力做功，因此小球的机械能的增量即为恒力F做的功．所以由功的表达式，求出恒力做功，从而求出小球机械能改变量．
（2）将小球的运动看成水平方向匀速与竖直方向匀加速运动，分别用位移与时间关系，从而求出2s时的两方向的位移大小，再进行合成．用速度与时间关系，同理可求出速度的大小及方向．
解答：解：（1）竖直方向上小球的加速度：
2s时竖直速度：Vy=at=3m/s
上升的竖直高度：
此过程中小球的机械能的改变量：△E=Fh=69J
（2）水平位移：x=Vt=8m
2s时的速度：大小
与水平方向夹角：
位移大小：
=
与水平方向夹角：
答：（1）此过程中小球的机械能改变量为69J；
（2）2s时小球的位移的大小为
，方向与水平方向夹角的正切为
；
速度的大小为5m/s，方向与水平夹角的正切为
．
点评：灵活考查了类平抛运动：水平方向做匀速直线运动，竖直方向做初速度为零的匀加速直线运动．同时涉及到运动学公式与运动的合成．
（2）将小球的运动看成水平方向匀速与竖直方向匀加速运动，分别用位移与时间关系，从而求出2s时的两方向的位移大小，再进行合成．用速度与时间关系，同理可求出速度的大小及方向．
解答：解：（1）竖直方向上小球的加速度：
2s时竖直速度：Vy=at=3m/s
上升的竖直高度：
此过程中小球的机械能的改变量：△E=Fh=69J
（2）水平位移：x=Vt=8m
2s时的速度：大小
与水平方向夹角：
位移大小：
=与水平方向夹角：
答：（1）此过程中小球的机械能改变量为69J；
（2）2s时小球的位移的大小为
，方向与水平方向夹角的正切为；速度的大小为5m/s，方向与水平夹角的正切为
．点评：灵活考查了类平抛运动：水平方向做匀速直线运动，竖直方向做初速度为零的匀加速直线运动．同时涉及到运动学公式与运动的合成．
练习册系列答案
名校课堂系列答案
相关题目
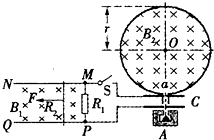如图所示，光滑且足够长的平行导轨MN和PQ固定在同一水平面上，两导轨间距L=0.2m，电阻R1=0.4Ω，导轨上静止放置一质量m=0.1kg，电阻R2=0.1Ω的金属杆，导轨电阻忽略不计，整个装置处在磁感应强度B1=0.5T的匀强磁场中，磁场的方向竖直向下，现用一外力F沿水平方向拉杆，使之由静止开始做匀加速运动并开始计时，若5s末杆的速度为2.5m/s，求：
一足够长的竖直圆筒，质量为m=2kg的小球恰能放入圆筒中，小球只要在圆筒内就能受到一竖直向上的作用恒力F=23N，最初小球在圆筒的底部且静止．现让圆筒以速度V0=4m/s水平向右匀速运动2s．重力加速度g=10m/s2．求：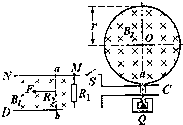
如图所示，光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上，两导轨间距离L=0.2m，电阻R1=0.4Ω，导轨上静止放置一质量m=0.1kg，电阻R2=0.1Ω的金属杆ab，导轨电阻忽略不计，整个装置处在磁感应强度B1=0.5T的匀强磁场中，磁场的方向竖直向下，现用一外力F沿水平方向拉杆ab，使之由静止开始运动，最终以8m/s的速度做匀速直线运动．若此时闭合开关S，释放的α粒子经加速电场C加速从a孔对着圆心O进入半径r=
如图所示，竖直放置的平行金属板M和N，它们的中央各有一个小孔O1、O2，上端接有阻值为2R的电阻，下端分别与竖直放置的足够长的光滑金属导轨连接（金属板及导轨电阻不计），它们间距离为L，导轨处在大小为B，方向垂直纸面向里的匀强磁场中．金属板M的左侧有直径为L，内壁光滑绝缘弹性圆筒，圆筒水平放置，筒内有如图所示的匀强磁场，筒壁开有小孔a，a、O1、O2与圆筒轴线上点O3在同一水平线上．现使质量为M、长度为L、电阻值为R导体棒PQ沿导轨从静止开始下滑，下滑过程中PQ始终与导轨接触良好．求：