题目内容
9. 如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=1.25m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)
如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=1.25m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)(1)每一滴水离开容器后经过多长时间滴落到盘面上?
(2)要使每一滴水在盘面上的落点都位于同一直线上,圆盘的角速度应为多大?
(3)当圆盘的角速度为2πrad/s时,第二滴水与第三滴水在盘面上落点间的距离2m,求容器的加速度a为多大?
分析 (1)离开容器后,每一滴水在竖直方向上做自由落体运动,水平方向做匀加速直线运动,水滴运动的时间等于竖直方向运动的时间,由高度决定;
(2)要使每一滴水在盘面上的落点都位于同一直线上,则圆盘在t秒内转过的弧度为kπ,k为不为零的正整数;
(3)通过匀加速直线运动的公式求出两个水滴在水平方向上的位移,再算出两个位移之间的夹角,根据位移关系算出容器的加速度.
解答 解:(1)由于离开容器后,每一滴水在竖直方向上做自由落体运动.
所以每一滴水滴落到盘面上所用时间$t=\sqrt{\frac{2h}{g}}$
(2)因为使每一滴水在盘面上的落点都位于同一直线,则圆盘在t秒内转过的弧度为kπ,k为不为零的正整数.
所以:ωt=kπ
即$ω=kπ\sqrt{\frac{g}{2h}}$,其中k=1,2,3…
(3)因为二滴水离开O点的距离为${s_2}=\frac{1}{2}a{t^2}+(at)t$…①
第三滴水离开O点的距离为${s}_{3}=\frac{1}{2}a{t}^{2}+(a2t)t$…②
(上面①②两式中:$t=\sqrt{\frac{2h}{g}}$…③)
又:$△θ=ωt=\frac{3}{2}π\sqrt{\frac{g}{2h}}×\sqrt{\frac{2h}{g}}=\frac{3}{2}π$
即第二滴水和第三滴水分别滴落在圆盘上x轴方向及垂直x轴的方向上.
则:s22+s32=s2…④
联列①②③④可得:$a=\frac{{\sqrt{73}}}{73}\frac{sg}{h}=0.117\frac{sg}{h}$.
答:(1)每一滴水离开容器后经过$\sqrt{\frac{2h}{g}}$时间滴落到盘面上;
(2)要使每一滴水在盘面上的落点都位于同一直线上,圆盘的角速度ω应为$kπ\sqrt{\frac{g}{2h}}$,其中k=1,2,3…;
(3)容器的加速度a为$0.117\frac{sg}{h}$.
点评 该题涉及到运动的合成与分解,圆周运动,匀变速直线运动的相关规律,特别注意水滴离开容器后做平抛运动,竖直方向做自由落体运动,水平方向做匀速直线运动,综合性较强,难度较大.

| A. | PA=6.5 kg•m/s PB=5.5 kg•m/s | B. | PA=6 kg•m/s PB=6 kg•m/s | ||
| C. | PA=5 kg•m/s PB=7 kg•m/s | D. | PA=4 kg•m/s PB=8 kg•m/s |
 一个质点A在光滑的水平面上运动,它受到另一个固定质点B的排斥力的作用,已知质点A的轨迹如图中的曲线所示,图中P、Q两点为轨迹上的点,虚线是过P、Q两点并与轨迹相切的中线,两虚线和轨迹平面分成四个区域,判断质点B的可能位置,下列说法中正确的是( )
一个质点A在光滑的水平面上运动,它受到另一个固定质点B的排斥力的作用,已知质点A的轨迹如图中的曲线所示,图中P、Q两点为轨迹上的点,虚线是过P、Q两点并与轨迹相切的中线,两虚线和轨迹平面分成四个区域,判断质点B的可能位置,下列说法中正确的是( )| A. | 可能在④区域,而不可能在①②③区域 | B. | 可能在①区域,而不可能在②③④区域 | ||
| C. | 可能在①②区域,而不可能在③④区域 | D. | 可能在①②④区域,而不可能在③区域 |
| A. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加之和代表物体的位移,这里采用了微元法 | |
| B. | 牛顿进行了“月-地检验”,得出天上和地下的物体都遵从万有引力定律的结论 | |
| C. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| D. | 由于牛顿在万有引力定律方面的杰出成就,所以被称为能“称量地球质量”的人 |
| A. | 关于光的本性,牛顿提出了“微粒说”,惠更斯提出了“波动说”,爱因斯坦提出了“光子说”,综合他们的说法圆满地说明了光的本性 | |
| B. | 光具有波粒二象性是指既可以把光看成宏观概念上的波,也可以看成微观概念上的粒子 | |
| C. | 光的干涉、衍射现象说明光具有波动性,光电效应和康普顿效应说明光具有粒子性 | |
| D. | 频率低、波长长的光,粒子性特征显著;频率高、波长短的光,波动性特征显著 |
 如图是一正在原地转动的坨螺,关于坨螺边缘上的A点和坨螺中间上的B点的运动,下列说法正确的是( )
如图是一正在原地转动的坨螺,关于坨螺边缘上的A点和坨螺中间上的B点的运动,下列说法正确的是( )| A. | A、B两点的线速度大小相等 | B. | A、B两点的角速度相同 | ||
| C. | A、B两点的向心加速度相同 | D. | A、B两点的向心力相同 |
 (合速度与合位移中分速度和分位移要求展开写)
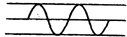
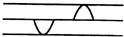
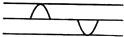
(合速度与合位移中分速度和分位移要求展开写)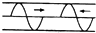 从一条弦线的两端,各发出一如图所示的脉冲横波,它们均沿弦线传播,速度相等,传播方向相反,在它们传播过程中,可能出现的脉冲波形是下图中( )
从一条弦线的两端,各发出一如图所示的脉冲横波,它们均沿弦线传播,速度相等,传播方向相反,在它们传播过程中,可能出现的脉冲波形是下图中( )