题目内容
9. 一个带负电的电荷量为q、质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( )
一个带负电的电荷量为q、质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( )| A. | 小球不能过B点 | |
| B. | 小球仍恰好能过B点 | |
| C. | 小球能过B点,且在B点与轨道之间压力不为0 | |
| D. | 小球在B点与轨道之间压力为0 |
分析 没有电场时,小球恰能通过轨道的最高点时恰好由重力提供向心力.加上电场时,运用动能定理分析到最高点时速度,研究向心力,判断能否通过最高点.
解答 解:没有电场时,最高点速度设为v,在最高点,由牛顿第二定律得:mg=m$\frac{{v}^{2}}{R}$,根据机械能守恒定律得:mg(h-2R)=$\frac{1}{2}$mv2,解得:h=$\frac{5}{2}$R,
加上电场时,恰好过最高点需要的速度设为v′,由牛顿第二定律得:mg-qE=m$\frac{v{′}^{2}}{R}$,解得:v′=$\sqrt{\frac{(mg-qE)R}{m}}$,
由动能定理得:mg(h-2R)-qE(h-2R)=$\frac{1}{2}$mv′2,解得:v′=$\sqrt{\frac{(mg-qE)R}{m}}$,说明小球仍恰好能过B点,且在B点与轨道之间没有压力,即压力为0,故AC错误,BD正确;
故选:BD
点评 本题考查了判断小球能否经过B点及球与轨道间是否有压力,本题是动能定理和向心力知识相结合的综合题,分析清楚小球的运动过程及小球过最高点的临界速度是解题的关键,应用牛顿第二定律与动能定理可以解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 用细线栓一小球在光滑平面上绕固定点做圆周运动,如图所示,则小球受到的力有( )
用细线栓一小球在光滑平面上绕固定点做圆周运动,如图所示,则小球受到的力有( )
 用细线栓一小球在光滑平面上绕固定点做圆周运动,如图所示,则小球受到的力有( )
用细线栓一小球在光滑平面上绕固定点做圆周运动,如图所示,则小球受到的力有( )| A. | 重力、桌面的支持力 | |
| B. | 只受向心力 | |
| C. | 重力、桌面的支持力、细线拉力和向心力 | |
| D. | 重力、桌面的支持力、细线拉力 |
17. 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固体电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )| A. | 电阻R1消耗的热功率为$\frac{Fv}{3}$ | |
| B. | 电阻R2消耗的热功率为$\frac{Fv}{6}$ | |
| C. | 整个装置因摩擦而消耗的热功率为μmgvcosθ | |
| D. | 整个装置消耗的电功率为Fv |
19.下列粒子从传送带为零的状态经过加速电压为U的电场加速之后,哪种粒子的速度最大?(选项括号中符号的左下角标为粒子所带的电荷数,左上角标为粒子的质量数)( )
| A. | 质子(${\;}_{1}^{1}$ H) | B. | 氘核(${\;}_{1}^{2}$H) | C. | α粒子(${\;}_{2}^{4}$ He) | D. | 钠离子(${\;}_{1}^{23}$Na) |
 在如图所示的匀强电场中,有一细线AB,B端固定有一个大小可忽略,质量为m,带电荷量为Q的小球,当B球静止后与竖直方向的夹角为θ,求匀强电场的场强.及小球所受的拉力大小.
在如图所示的匀强电场中,有一细线AB,B端固定有一个大小可忽略,质量为m,带电荷量为Q的小球,当B球静止后与竖直方向的夹角为θ,求匀强电场的场强.及小球所受的拉力大小.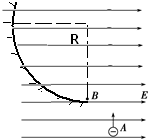 如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求:
如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求: 如图所示,两带电平行板竖直放置,开始时两极板间电压为U,相距为d,两极板间形成匀强电场.有一带电粒子,质量为m(重力不计)、所带电荷量为+q,从两极板下端连线的中点P以竖直速度v0射入匀强电场中,带电粒子落在A极板的M点上.
如图所示,两带电平行板竖直放置,开始时两极板间电压为U,相距为d,两极板间形成匀强电场.有一带电粒子,质量为m(重力不计)、所带电荷量为+q,从两极板下端连线的中点P以竖直速度v0射入匀强电场中,带电粒子落在A极板的M点上. 如图所示的空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.求:
如图所示的空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.求: 如图所示,在匀强电场中,电场线与水平方向成θ角,一电荷量为q、质量为m的带电小球,用长为l的绝缘细线悬挂于O点,当小球静止时,细线恰好呈水平状态,现给小球一垂直于细线的初速度使小球恰好在竖直平面内做圆周运动,重力加速度为g,求:
如图所示,在匀强电场中,电场线与水平方向成θ角,一电荷量为q、质量为m的带电小球,用长为l的绝缘细线悬挂于O点,当小球静止时,细线恰好呈水平状态,现给小球一垂直于细线的初速度使小球恰好在竖直平面内做圆周运动,重力加速度为g,求: