题目内容
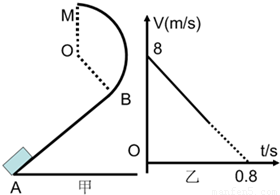
如图甲所示,一半径为R=0.1m,竖直圆弧形光滑轨道,与斜面相切与B处,圆弧的最高点为M,斜面倾角为60°,t=0时刻,有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,物块质量m=1千克,若物块恰能到M点(g=10m/s2)求:(1)物块经过B点时的速度VB;
(2)物块在斜面上滑动的过程中摩擦力做功的平均功率.
【答案】分析:(1)、分析物块的运动过程,要求B点时的速度,则分析从B到M的运动,从力做功看机械能守恒,则 m
m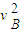 -
- m
m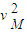 =mgh,那么由几何关系求出h,在M点由牛顿第二定律求出vM,这样就可求出B点的速度.
=mgh,那么由几何关系求出h,在M点由牛顿第二定律求出vM,这样就可求出B点的速度.
(2)、在斜面上求摩擦力的平均功率,首先由速度图象得出加速度和初速度,分析物块的受力,由牛顿第二定律求出摩擦力,由运动学公式求出平均速度,即可用功率的计算式得摩擦力的平均功率.
解答:解:(1)、由题中的几何关系知圆弧对应的圆心角为120°
∴物块从B到M上升的高度为h=R+Rcos60°
物块恰能过最高点,则在M点由牛顿第二定律得:mg=m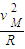
物块从B到M的过程中机械能守恒,由机械能守恒定律得:
 m
m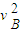 -
- m
m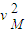 =mgh
=mgh
联立以上各式解得物块经过B点时的速度为:vB=2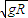 =2×
=2×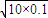 m/s=2m/s
m/s=2m/s
(2)、分析速度图象求知物块在斜面上的加速度为:a=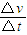 =
=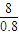 m/s2=10m/s2
m/s2=10m/s2
在斜面上对物块由牛顿第二定律得:mgsinθ+f=ma
∴摩擦力f=ma-mgsinθ=(10-5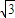 )N
)N
物块在斜面上的平均速度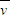 =
=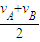 =
=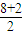 m/s=5m/s
m/s=5m/s
∴摩擦力的平均功率为:P=f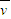 =(10-5
=(10-5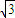 )×5W=6.7W
)×5W=6.7W
答:(1)物块经过B点时的速度vB为2m/s;(2)物块在斜面上滑动的过程中摩擦力做功的平均功率是6.7W.
点评:解答此题需结合速度图象分析物块从B到M和从A到B两过程的受力和运动特点,抓住在M点的临界条件:压力为零,然后利用几何关系、牛顿第二定律、机械能守恒定律求B点的速度.求摩擦力的平均功率需从功率计算式入手,进而求出从A到B的摩擦力与平均速度即可求出.
 m
m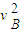 -
- m
m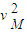 =mgh,那么由几何关系求出h,在M点由牛顿第二定律求出vM,这样就可求出B点的速度.
=mgh,那么由几何关系求出h,在M点由牛顿第二定律求出vM,这样就可求出B点的速度.(2)、在斜面上求摩擦力的平均功率,首先由速度图象得出加速度和初速度,分析物块的受力,由牛顿第二定律求出摩擦力,由运动学公式求出平均速度,即可用功率的计算式得摩擦力的平均功率.
解答:解:(1)、由题中的几何关系知圆弧对应的圆心角为120°
∴物块从B到M上升的高度为h=R+Rcos60°
物块恰能过最高点,则在M点由牛顿第二定律得:mg=m
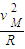
物块从B到M的过程中机械能守恒,由机械能守恒定律得:
 m
m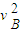 -
- m
m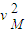 =mgh
=mgh联立以上各式解得物块经过B点时的速度为:vB=2
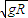 =2×
=2×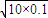 m/s=2m/s
m/s=2m/s(2)、分析速度图象求知物块在斜面上的加速度为:a=
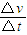 =
=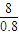 m/s2=10m/s2
m/s2=10m/s2在斜面上对物块由牛顿第二定律得:mgsinθ+f=ma
∴摩擦力f=ma-mgsinθ=(10-5
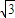 )N
)N物块在斜面上的平均速度
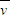 =
=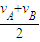 =
=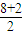 m/s=5m/s
m/s=5m/s∴摩擦力的平均功率为:P=f
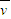 =(10-5
=(10-5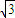 )×5W=6.7W
)×5W=6.7W答:(1)物块经过B点时的速度vB为2m/s;(2)物块在斜面上滑动的过程中摩擦力做功的平均功率是6.7W.
点评:解答此题需结合速度图象分析物块从B到M和从A到B两过程的受力和运动特点,抓住在M点的临界条件:压力为零,然后利用几何关系、牛顿第二定律、机械能守恒定律求B点的速度.求摩擦力的平均功率需从功率计算式入手,进而求出从A到B的摩擦力与平均速度即可求出.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图甲所示,一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能达到M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:
如图甲所示,一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能达到M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求: 如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,若物块恰能到达M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:
如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=37°,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,若物块恰能到达M点,(取g=10m/s2,sin37°=0.6,cos37°=0.8),求: (2011?河南三模)如图甲所示,一半径为R=0.1m,竖直圆弧形光滑轨道,与斜面相切与B处,圆弧的最高点为M,斜面倾角为60°,t=0时刻,有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,物块质量m=1千克,若物块恰能到M点(g=10m/s2)求:
(2011?河南三模)如图甲所示,一半径为R=0.1m,竖直圆弧形光滑轨道,与斜面相切与B处,圆弧的最高点为M,斜面倾角为60°,t=0时刻,有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示,物块质量m=1千克,若物块恰能到M点(g=10m/s2)求: