题目内容
14.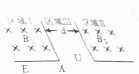 如图所示是某中学学生根据回旋加速器原理设计的一个小型粒子加速器的原理示意图,区域Ⅰ和区域Ⅱ存在匀强磁场B1和B2.在宽度为d的区域Ⅲ内存在一个匀强电场,电势差大小为U,通过自动调整两区域间的电势高低可使进入该区域的电势差大小恒为U,通过自动调整两区域间的电势高低可使进入该区域的粒子持续加速.在图中A位置静止释放一个质量为m,带电量为q的正电粒子(重力不计),粒子经过两次电场加速后最终垂直于区域Ⅰ边缘AE射出,一切阻力不计,求:
如图所示是某中学学生根据回旋加速器原理设计的一个小型粒子加速器的原理示意图,区域Ⅰ和区域Ⅱ存在匀强磁场B1和B2.在宽度为d的区域Ⅲ内存在一个匀强电场,电势差大小为U,通过自动调整两区域间的电势高低可使进入该区域的电势差大小恒为U,通过自动调整两区域间的电势高低可使进入该区域的粒子持续加速.在图中A位置静止释放一个质量为m,带电量为q的正电粒子(重力不计),粒子经过两次电场加速后最终垂直于区域Ⅰ边缘AE射出,一切阻力不计,求:(1)粒子进入区域Ⅰ和区域Ⅱ的速度之比
(2)区域Ⅰ和区域Ⅱ的磁感应强度之比
(3)已知区域Ⅰ的磁感应强度B1=B0,求从粒子释放到从区域Ⅰ边缘飞出的总时间.
分析 (1)根据动能定理求出粒子进入区域Ⅰ和区域Ⅱ的速度,再求比值;
(2)画出轨迹,根据几何关系得到半径关系,根据半径公式求磁感应强度之比;
(3)求出粒子在电场和磁场中的运动时间即为粒子释放到从区域Ⅰ边缘飞出的总时间
解答  解:(1)设粒子进入区域Ⅱ的速度为${v}_{Ⅱ}^{\;}$,根据动能定理有:
解:(1)设粒子进入区域Ⅱ的速度为${v}_{Ⅱ}^{\;}$,根据动能定理有:
$qU=\frac{1}{2}m{v}_{Ⅱ}^{2}-0$
解得:${v}_{Ⅱ}^{\;}=\sqrt{\frac{2qU}{m}}$
设粒子进入区域Ⅰ的速度为${v}_{Ⅰ}^{\;}$,根据动能定理,有:
$qU=\frac{1}{2}m{v}_{Ⅰ}^{2}-\frac{1}{2}m{v}_{Ⅱ}^{2}$
解得:${v}_{Ⅰ}^{\;}=\sqrt{\frac{4qU}{m}}$
所以粒子进入区域Ⅰ和Ⅱ的速度之比为:$\frac{{v}_{Ⅰ}^{\;}}{{v}_{Ⅱ}^{\;}}=\sqrt{2}$
(2)画出粒子运动的轨迹,如图所示,由图可知,在区域Ⅰ中的轨道半径是区域Ⅱ中轨道半径的2倍,由半径公式有:
$R=\frac{mv}{qB}$
得:$B=\frac{mv}{qR}$
$\frac{{B}_{Ⅰ}^{\;}}{{B}_{Ⅱ}^{\;}}=\frac{{v}_{Ⅰ}^{\;}}{{v}_{Ⅱ}^{\;}}•\frac{{R}_{Ⅱ}^{\;}}{{R}_{Ⅰ}^{\;}}=\sqrt{2}×\frac{1}{2}=\frac{\sqrt{2}}{2}$
(3)区域Ⅰ的磁感应强度B1=${B}_{0}^{\;}$,区域Ⅱ的磁感应强度由(2)知,${B}_{Ⅱ}^{\;}=\sqrt{2}{B}_{0}^{\;}$
粒子由静止到区域Ⅱ的时间为:$d=\frac{{v}_{Ⅱ}^{\;}}{2}{t}_{1}^{\;}$,
得:${t}_{1}^{\;}=\frac{2d}{{v}_{Ⅱ}^{\;}}=2d\sqrt{\frac{m}{2qU}}=d\sqrt{\frac{2m}{qU}}$=$\sqrt{2}d\sqrt{\frac{m}{qU}}$
在磁场区域Ⅱ中的时间为:${t}_{2}^{\;}=\frac{1}{2}{T}_{Ⅱ}^{\;}=\frac{πm}{q{B}_{Ⅱ}^{\;}}=\frac{πm}{\sqrt{2}q{B}_{0}^{\;}}$
第二次在电场中加速的时间为:$d=\frac{1}{2}(\sqrt{\frac{2qU}{m}}+\sqrt{\frac{4qU}{m}}){t}_{3}^{\;}$,
得:${t}_{3}^{\;}=\frac{2d}{2+\sqrt{2}}\sqrt{\frac{m}{qU}}=(2-\sqrt{2})d\sqrt{\frac{m}{qU}}$
在磁场区域Ⅰ中运动的时间为:${t}_{4}^{\;}=\frac{1}{4}\frac{2πm}{q{B}_{0}^{\;}}=\frac{πm}{2q{B}_{0}^{\;}}$
从粒子释放到从区域Ⅰ边缘飞出的总时间为:t=$\frac{\sqrt{2}+1}{2}\frac{πm}{q{B}_{0}^{\;}}+2d\sqrt{\frac{m}{qU}}$
答:(1)粒子进入区域Ⅰ和区域Ⅱ的速度之比$\sqrt{2}$
(2)区域Ⅰ和区域Ⅱ的磁感应强度之比$\sqrt{2}:2$
(3)已知区域Ⅰ的磁感应强度B1=B0,从粒子释放到从区域Ⅰ边缘飞出的总时间$\frac{\sqrt{2}+1}{2}\frac{πm}{q{B}_{0}^{\;}}+2d\sqrt{\frac{m}{qU}}$
点评 解决该题的关键是根据题目的要求,正确画出粒子运动的轨迹,并根据几何关系写出粒子的半径与磁场的半径的关系.记住粒子在磁场中匀速圆周运动的周期公式和半径公式.

 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )| A. | 人拉绳行走的速度为vsinθ | B. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C. | 船的加速度为 $\frac{Fcosθ-f}{m}$ | D. | 船的加速度为 $\frac{F-f}{m}$ |
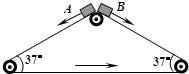 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 物块AB同时到达传送带底端 | |
| C. | 传送带对物块AB的摩擦力都沿传送带向上 | |
| D. | 物块A下滑过程中相对传送带的位移小于物块B下滑过程中相对传送带的位移 |
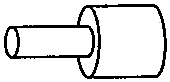
| A. | 相同时间内通过任一横截面的电荷量相等 | |
| B. | 相同时间内通过粗棒横截面的电荷量多 | |
| C. | 细棒与粗棒两端的电压相等 | |
| D. | 细棒两端的电压大于粗棒两端的电压 |
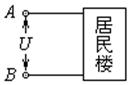 如图所示,一幢居民楼里住着生活水平各不相同的24户居民,所以整幢居民楼里有各种不同的电器,例如电炉、电视机、微波炉、电脑等等.供电后,各家电器同时使用,A、B间的电阻为R,A、B间的电压为U,进线电流为I,如图所示,则计算该幢居民楼用电的总功率可以用的公式是( )
如图所示,一幢居民楼里住着生活水平各不相同的24户居民,所以整幢居民楼里有各种不同的电器,例如电炉、电视机、微波炉、电脑等等.供电后,各家电器同时使用,A、B间的电阻为R,A、B间的电压为U,进线电流为I,如图所示,则计算该幢居民楼用电的总功率可以用的公式是( )| A. | P=I2R | B. | P=$\frac{{U}^{2}}{R}$ | C. | P=UI | D. | 无法计算 |
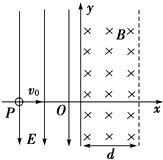 如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求:
如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求: 质谱仪的工作原理如图示,一个质量为m,电荷量为 q的带正电粒子,经过电压为U的加速电场由静止加速后,刚好直线进入速度选择器.速度选择器内有相互垂直的匀强磁场和匀强电场E.直线通过选择器的粒子经狭缝P后进入到偏转磁场,最后打在胶片A1A2上,且离P点的距离为L.求:
质谱仪的工作原理如图示,一个质量为m,电荷量为 q的带正电粒子,经过电压为U的加速电场由静止加速后,刚好直线进入速度选择器.速度选择器内有相互垂直的匀强磁场和匀强电场E.直线通过选择器的粒子经狭缝P后进入到偏转磁场,最后打在胶片A1A2上,且离P点的距离为L.求: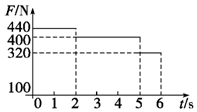 一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2)
一质量为m=40kg的小孩站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.求在这段时间内电梯上升的高度是多少(取重力加速度g=10m/s2) 一个电子(质量为9.1×10-31kg,电荷量为1.6×10-19C)以v0=7×107m/s的初速度沿着匀强电场的电场线方向飞入匀强电场,已知匀强电场的电场强度大小E=2×105N/C,不计重力,求:
一个电子(质量为9.1×10-31kg,电荷量为1.6×10-19C)以v0=7×107m/s的初速度沿着匀强电场的电场线方向飞入匀强电场,已知匀强电场的电场强度大小E=2×105N/C,不计重力,求: